2020. 8. 9. 13:52ㆍML in Python/Python
이 게시글은 오로지 파이썬을 통한 실습만을 진행한다. K-means 군집분석의 개념 및 원리를 알고자하면 아래 링크를 통해학습을 진행하면 된다. 아래는 3개의 실습과정을 통해서 k-means 공부를 진행할 것이다. 각 단계에서 사용되는 parameter는 약간의 차이가 있다. 그렇기에 하나씩 읽어나가면 k-means의 구현과정을 알아가는데 많은 도움이 될 것이라고 생각한다. 그렇기에 모든 실습과정을 살펴보는 것을 추천한다.
https://todayisbetterthanyesterday.tistory.com/58
[Data Analysis 개념] Clustering(1) - K-means/K-medoids
1. Clustering - 군집분석 군집분석은 비지도학습(unsupervised learning)의 일종으로 유사한 데이터끼리 그룹화를 시키는 학습모델을 말한다. 각 데이터의 유사성을 측정하여, 유사성이 높은 집단끼리 �
todayisbetterthanyesterday.tistory.com
라이브러리와 데이터 로드
# library
from sklearn import datasets
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans
# data
iris = datasets.load_iris()
# feature&target
X = iris.data[:, :2]
y = iris.targetKmeans clustering의 함수는 sklear.cluster 라이브러리에서 찾을 수 있다. 또한 실습 진행을 위해서 iris dataset를 load하고 실습의 간편성을 위해서 iris feature의 Sepal Width와 Sepal Length만 사용할 것이다.
Raw data 확인
# raw data cmap
plt.scatter(X[:,0], X[:,1], c=y, cmap='gist_rainbow')
plt.xlabel('Spea1 Length', fontsize=18)
plt.ylabel('Sepal Width', fontsize=18)
위의 그림은 raw data를 cmap을 통해서 나타낸 것이다. 위를 보면 빨간색 데이터는 비교적 구분이 잘 되어 있다. 반면 연두색과 분홍색으로 표시된 cluster는 중첩되어있는 것을 확인할 수 있다. 이를 유의하고 실습을 진행해보자.
K-mean fitting
km = KMeans(n_clusters = 3, n_jobs = 4, random_state=21)
km.fit(X)
n_clusters 인수는 k-means의 k를 의미하는 군집형성의 개수를 뜻한다.
n_jobs는 scikit-learn의 기본적인 병렬처리로 내부적으로 멀티프로세스를 사용하는 것이다. 만약 CPU 코어의 수가 충분하다면 n_jobs를 늘릴수록 속도가 증가한다.
random_state를 통해서 난수 고정을 하였다. 학습결과의 동일성을 위해서이다. km변수에 k-means모델을 정의하고 학습을 진행하였다.
centers = km.cluster_centers_
print(centers)
학습된 kmeans모델은 centroids를 갖는다. 이는 군집의 중심점이란 것이다. 이를 수치적으로 출력하기 위해서는 .cluster_centers_ 라는 함수를 통해서 좌표값을 확인할 수 있다.
결과 비교시각화
new_labels = km.labels_
# Plot the identified clusters and compare with the answers
fig, axes = plt.subplots(1, 2, figsize=(16,8))
axes[0].scatter(X[:, 0], X[:, 1], c=y, cmap='gist_rainbow',
edgecolor='k', s=150)
axes[1].scatter(X[:, 0], X[:, 1], c=new_labels, cmap='jet',
edgecolor='k', s=150)
axes[0].set_xlabel('Sepal length', fontsize=18)
axes[0].set_ylabel('Sepal width', fontsize=18)
axes[1].set_xlabel('Sepal length', fontsize=18)
axes[1].set_ylabel('Sepal width', fontsize=18)
axes[0].tick_params(direction='in', length=10, width=5, colors='k', labelsize=20)
axes[1].tick_params(direction='in', length=10, width=5, colors='k', labelsize=20)
axes[0].set_title('Actual', fontsize=18)
axes[1].set_title('Predicted', fontsize=18)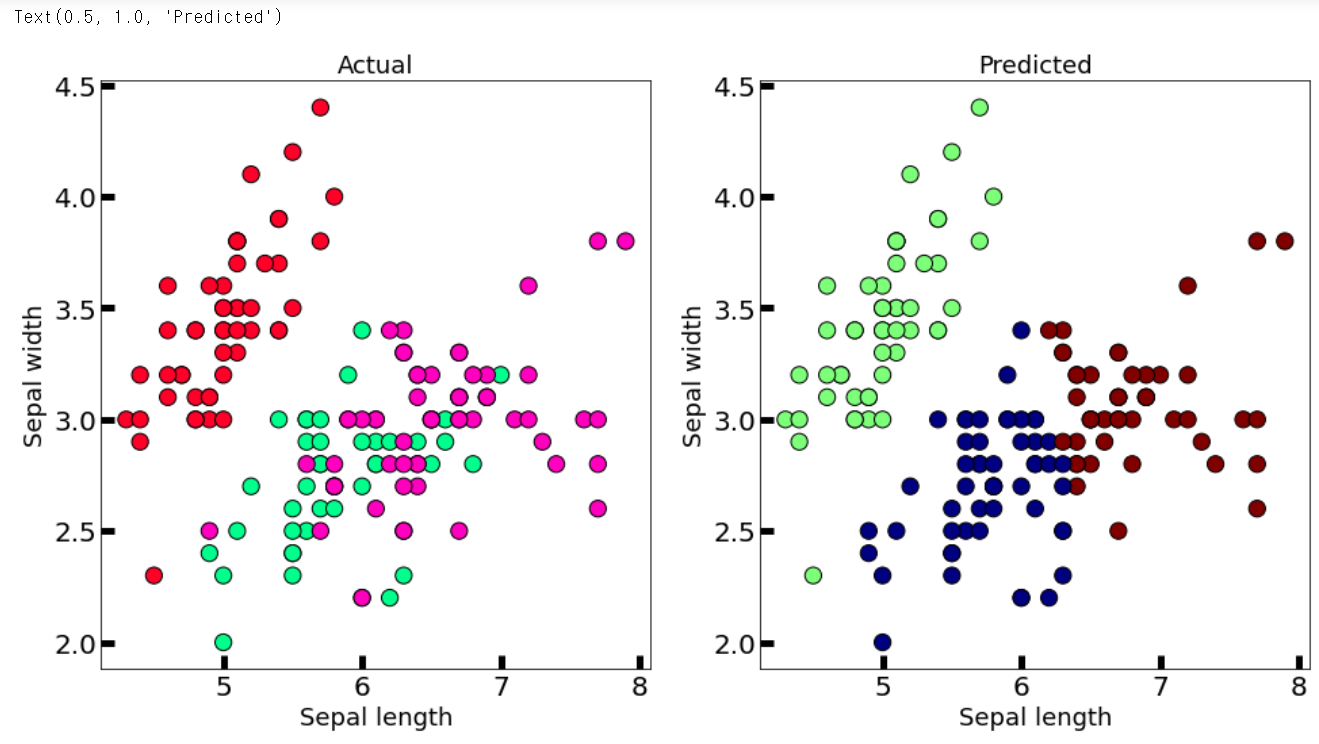
raw data의 cmap과 k-means를 통해 학습완료되어 군집을 형성한 군집분류된 cmap의 결과를 axes 분리를 통해서 동시에 나타내었다. 이를 통해서 확인한 결과 기존의 빨간데이터는 비교적 동떨어져있어서 분리가 확실하게 된 것을 확인할 수 있다.
하지만, 중첩된 데이터(연두색과 분홍색)의 경우 군집의 형성은 잘 되었으나, 중첩된 부분이 크기에 제대로 분류가 일어나지 않았다. 이것이 k-means를 포함한 군집분석에 가장 큰 약점이다.
더욱이 k-means의 경우에는 원형관계가 아니라면 분석이 제대로 일어나지 않는다는 단점이 있다. 즉 세로로 | | | 분포되어있는 데이터를 k-means를 통해서 분석할 경우 제대로 군집형성이 이루어지지 않을 가능성이 높다는 것이다. 비교적 이를 해결한 것이 DBSCAN모델이다. 이는 나중에 알아보도록하고 새로운 원형군집의 데이터셋을 만들어서 확인해보자.
두 번째 실습데이터 형성 (원형군집)
from sklearn.datasets import make_blobs
# create dataset
X, y = make_blobs(
n_samples=150, n_features=2,
centers=3, cluster_std=0.5,
shuffle=True, random_state=0
)
# plot
plt.scatter(
X[:, 0], X[:, 1],
c='white', marker='o',
edgecolor='black', s=50
)
plt.show()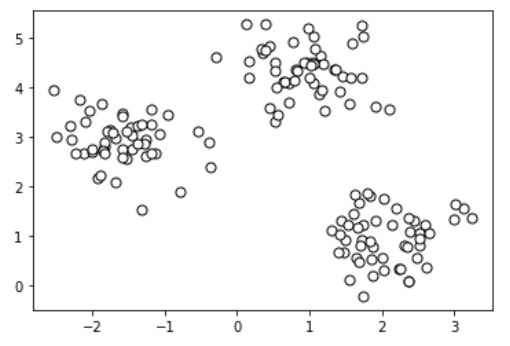
위에 코드를 보면 make_blobs함수를 통해서 150개의 샘플을 0.5의 표준편차를 가진 3개의 중심점으로 군집을 형성하였다. 이를 시각화 한 것이 위의 scatter plot이다.
두 번째 k-means 데이터 학습 및 결과
km = KMeans(
n_clusters=3, init='random',
n_init=10, max_iter=300,
tol=1e-04, random_state=0
)
y_km = km.fit_predict(X)
y_km
이를 다시 k-means를 통해서 학습을 시킨다. 위에서 추가된 parameter가 init / n_init / max_iter / tol 이 있다.
init 의 경우는 k-means가 중심점(centroid)를 기준으로 군집을 형성하는데 있어서 초기중심점을 random으로 설정한다는 것이다. 최근에는 init = "K-means++"을 사용하여 최적의 클러스터로 묶을 가능성을 높힌 알고리즘이 생겼다. "K-means++" 는 하나의 무작위 중심점을 배정하고 두번째 중심점을 첫번째 중심점과 멀리 떨어진 곳에 배치, 그리고 다음 중심점을 1,2번째 중심점과 멀리 떨어지도록 배치하는 방식이다. 즉, 중심점 선정에 있어서 무작위로 진행하는 것이 아니라 좀 더 신중하게 설정하는 것이다. 이런 방식을 통해서 k-means의 단점을 보완할 수 있다.
n_init은 초기 중앙점이 무작위로 선택되기에 가장 나은 결과를 얻기 위해 몇 번 초기값을 변경하여 알고리즘을 실시할 지를 정하는 것이다. 간단하게 표현하면 초기중심점 선택의 반복 횟수 알고리즘인 것이다.
max_iter는 학습의 최대 반복횟수를 의미한다.
tol은 max_iter의 반복횟수를 계속 하면 너무 많은 시간이 소요되기에, inertia (Sum of squared distances of samples to their closest cluster center)이 지정해준 tol만큼 줄어들지 않으면 조기에 종료시킨다는 것이다.
plt.scatter(
X[y_km == 0, 0], X[y_km == 0, 1],
s=50, c='lightgreen',
marker='s', edgecolor='black',
label='cluster 1'
)
plt.scatter(
X[y_km == 1, 0], X[y_km == 1, 1],
s=50, c='orange',
marker='o', edgecolor='black',
label='cluster 2'
)
plt.scatter(
X[y_km == 2, 0], X[y_km == 2, 1],
s=50, c='lightblue',
marker='v', edgecolor='black',
label='cluster 3'
)
# plot the centroids
plt.scatter(
km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
s=250, marker='*',
c='red', edgecolor='black',
label='centroids'
)
plt.legend(scatterpoints=1)
plt.grid()
plt.show()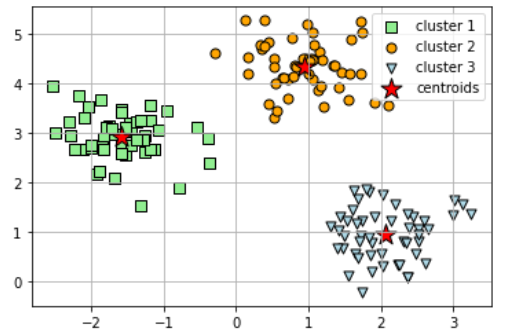
위의 원형군집을 k-means로 군집분석을 실시하여 가시화한 결과는 위와 같다. 우리는 3개의 군집을 형성한다는 parameter를 지정하여 3개의 중심점과 그 중심점을 기준으로 3개의 군집이 형성된 것을 확인할 수 있다. 여기서 문제가 있다. 이 중심점의 개수는 어떻게 정하나? 위와 같이 간단한 데이터여서 데이터를 보고 확인할 수 있었다면 매우 좋을 것이다.
하지만 현실데이터처럼 복잡한 데이터라면 이야기가 달라진다. 밑에는 k=4, 즉 4개의 군집을 형성하는 예시이다. 이를 먼저 확인해보자.
4개의 centroids K-means clustering
km = KMeans(
n_clusters=4, init='random',
n_init=10, max_iter=300,
tol=1e-04, random_state=0
)
y_km = km.fit_predict(X)plt.scatter(
X[y_km == 0, 0], X[y_km == 0, 1],
s=50, c='lightgreen',
marker='s', edgecolor='black',
label='cluster 1'
)
plt.scatter(
X[y_km == 1, 0], X[y_km == 1, 1],
s=50, c='orange',
marker='o', edgecolor='black',
label='cluster 2'
)
plt.scatter(
X[y_km == 2, 0], X[y_km == 2, 1],
s=50, c='lightblue',
marker='v', edgecolor='black',
label='cluster 3'
)
plt.scatter(
X[y_km == 3, 0], X[y_km == 3, 1],
s=50, c='lightblue',
marker='d', edgecolor='black',
label='cluster 4'
)
# plot the centroids
plt.scatter(
km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
s=250, marker='*',
c='red', edgecolor='black',
label='centroids'
)
plt.legend(scatterpoints=1)
plt.grid()
plt.show()
k를 제외하고 동일한 parameter를 정의하여 모델을 학습했다. 이를 시각화한 결과는 위와 같다. cluster3,4가 구분되기 힘들게 형성되었다. 그렇다면 최적의 k를 찾는 방법은 무엇이 있을까?
군집 내 분산을 확인하여 K를 정하는 방법
distortions = []
for i in range(1, 11):
km = KMeans(
n_clusters=i, init='random',
n_init=10, max_iter=300,
tol=1e-04, random_state=0
)
km.fit(X)
distortions.append(km.inertia_) # 군집 내 분산, 적을수록 좋음
# plot - 급격하게 줄어드는 부분
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()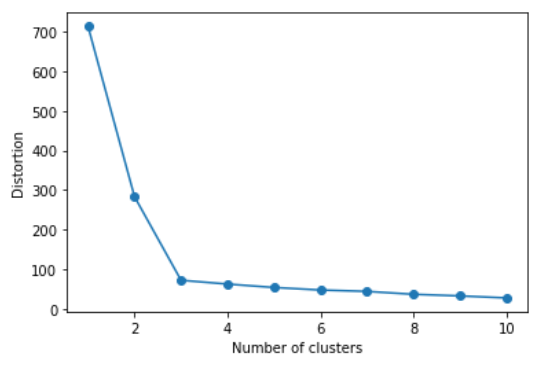
위의 코드는 range를 통해서 군집형성의 개수를 1개부터 10개까지 형성하여 반복학습을 진행한다. 그리고 각 군집의 개수 모델마다 군집 내 분산을 확인한다. 이때, 군집의 분산이 작을수록 좋은데 군집 내 분산이 완만하게 줄어드는 지점이 k=3이다. 군집이 증가하면 당연하게 증가할수록 당연하게 분산은 적어질 수밖에 없다. 하지만, 일정 수준 이상 줄어드는 것이 제대로된 군집형성을 의미하진 않는다.
그렇기에 최종적으로 k=3이 위의 데이터에서 가장 적절한 군집의 개수라고 볼 수 있다.
이제는 다른 실습을 진행할 것이다. vectorization을 통해서 자연어를 처리하는 방법 중 하나로 군집분석을 사용할 수 있다. 만약 기사를 분류해야하는데 경제/연예/정치 기사들이 있다면 어떻게 분류를 진행할 것인가?
기사데이터는 아니지만, 임의로 kitty / google / dog 문장을 만들었다. 그리고 이 문장들을 맞게 분류하는지 확인할 것이다.
Text Data를 통한 K-means clustering
from sklearn.cluster import KMeans
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics import adjusted_rand_score
documents = ["This little kitty came to play when I was eating at a restaurant.","hello kitty is my favorite character",
"Merley has the best squooshy kitten belly.","Is Google translator so good?","google google"
"google Translate app is incredible.","My dog s name is Kong","dog dog dog","cat cat"
"If you open 100 tab in google you get a smiley face.","Kong is a very cute and lovely dog",
"Best cat photo I've ever taken.","This is a cat house"
"Climbing ninja cat kitty.","What's your dog's name?","Cat s paws look like jelly",
"Impressed with google map feedback.","I want to join google","You have to wear a collar when you walk the dog",
"Key promoter extension for google Chrome.","Google is the best company","Google researcher"]
vectorizer = TfidfVectorizer(stop_words='english')
X = vectorizer.fit_transform(documents)
여기서 TfidVectorizer는 문장의 길이를 비교하여 vector화 시키는 방법이다.
X
이 vectorizer된 문서는 19X55의 sparse matrix로 형성된다.
true_k = 3
model = KMeans(n_clusters=true_k, init='k-means++', max_iter=100, n_init=1)
model.fit(X)
우리는 실습에서 분류할 대상을 kitty/google/dog으로 이미 알고있기에 true_k = 3을 정의했다.
order_centroids = model.cluster_centers_.argsort()[:, ::-1]
terms = vectorizer.get_feature_names()model.labels_

[x for x, y in zip(documents, model.labels_) if y == 0]

[x for x, y in zip(documents, model.labels_) if y == 1]
[x for x, y in zip(documents, model.labels_) if y == 2]

위의 결과를 보면 생각보다는 군집화가 잘 이루어졌다. kitty/dog/google의 군집에 이상값이 없어보인다. 물론 사실 너무 최적화시키기 쉬운 text를 형성하여 vectorization과 clustering을 실시했기에 그럴 수 있다.
Y = vectorizer.transform(["chrome browser to open."])
prediction = model.predict(Y)
print(prediction)
Y = vectorizer.transform(["I want to have a dog"])
prediction = model.predict(Y)
print(prediction)
Y = vectorizer.transform(["My cat is hungry."])
prediction = model.predict(Y)
print(prediction)
새로운 문장을 예측한 것 또한 그렇기에 잘 분류가 일어난다.
이상으로 k-means clustering의 실습을 마쳤다. K-medoids의 경우는 k-means가 평균을 기준으로 거리계산을 하여 군집을 형성하기에 이상값에 민감하다는 단점을 보완하고자, 중앙값(median)을 이용하여 거리기준의 군집분석을 수행하는 것이다. 큰 차이는 없다. 다음에는 hierarchical clustering과 DBSCAN을 구현하는 과정을 살펴보자.
'ML in Python > Python' 카테고리의 다른 글
| [Python] DBSCAN clustering (0) | 2020.08.09 |
|---|---|
| [Python] Hierarchical clustering(계층적 군집분석) (0) | 2020.08.09 |
| [Python] 중요변수를 추출하기 위한 방법 - Shap Value 구현 (6) | 2020.08.03 |
| [Python] Ensemble(앙상블) - Boosting(AdaBoost, Gradient Boosting) (0) | 2020.07.31 |
| [Python] Ensemble(앙상블) - Random Forest(랜덤포레스트) (0) | 2020.07.31 |