2020. 7. 24. 16:45ㆍADP | ADsP with R/Knowledge
이 게시글은 신경망 모형을 R로 구현하는 과정만 진행한다. 그렇기에 인경신경망에 대한 원리와 정확한 개념을 알기 위해서는 아래 링크를 통해서 학습하길 바란다.
https://todayisbetterthanyesterday.tistory.com/42
[Data Analysis 개념] 인공신경망(Artificial Neural Network) 모형의 원리와 구성 - Perceptron / Activation function
1. 인공 신경망 모형의 배경 인공 신경망 모형은 인간의 뉴련의 자극전달 과정에 아이디어를 착안하여 발생한 머신러닝 알고리즘이다. 인간의 뉴런은 시냅스를 통하여 다른 뉴런으로부터 자극
todayisbetterthanyesterday.tistory.com
1. Artificial Neural Network 요약
이번 게시글에서는 인공신경망(Artificial Neural Network)에 대한 개념을 다루지 않고 scikit learn라이브러리를 활용하여 Neural Network 모형을 구축해보는 실습을 진행할 것이다.
인공 신경망 모형은 인간의 뉴런을 모방하여 알고리즘으로 구현할 것을 말한다. 인간의 뉴런은 시냅스를 통하여 다른 여러 뉴런으로 부터 자극을 전달받고 이를 또다른 뉴런으로 전달시키는 과정을 거친다.
이 인간의 뉴런을 "퍼셉트론"이라는 인공 뉴런을 구성하고 이 퍼셉트론들이 여러 layer를 거치며 시냅스를 통한 자극의 전달과정을 모방한 것이 Neural Network이다.
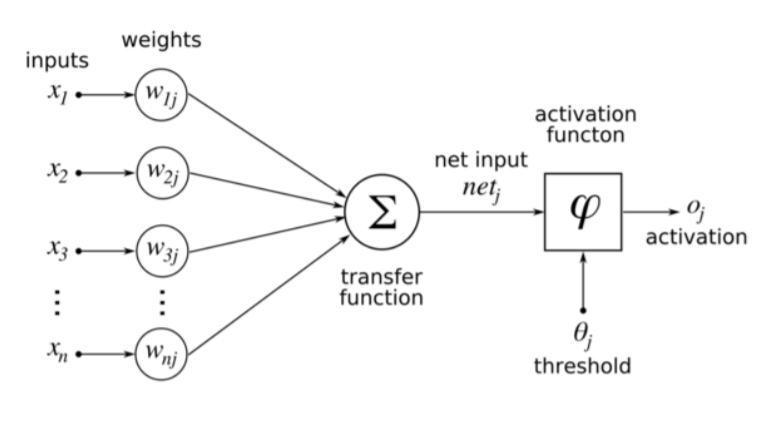
Neural Network에서는 가장 중요한 구성요소로 inputs / weights / activation function / error(bias) 를 꼽을 수 있다. Neural Network의 과정을 간략하게 말하자면, input layer에서 inputs값들이 여러개의 퍼셉트론으로 이루어진 다층 퍼셉트론 layer(이를 은닉층/Hidden Layer라고 한다)를 거치며 Weigths와 error를 활성화함수를 통해 조정하면서 학습을 진행해 Output layer로 결과를 출력하는 과정이다.
이때, activation function(활성화 함수)는 sigmoid function / ReLU / leaky ReLU / ELU 등 여러가지 존재하지만,
1. gradient vanishing 문제
2. 중간에 Global minimum을 찾지 못하고, local minimum에서 학습을 멈추는 문제
와 같은 이유로 ReLU관련 활성화 함수를 요즘은 많이 쓴다.
그 외 backpropagation 등 기본적인 원리에 많은 것들에 대한 설명이 필요하지만 자세한 수학적 원리와 과정은 다음 게시물을 통해서 다루겠다. Python에서 sklearn이라는 module을 통해서 실습을 진행해보자. 물론 keras와 tensorflow를 통해서 또한 진행할 수 있으나, sklearn은 머신러닝에 대해서 처음 접하는 사람이 쓰기 매우 편한 점이 모든 학습 모델과 적합 함수의 형태가 동일하다는 것이다. 여튼 이제 진행해보겠다.
2. R을 활용한 신경망 모형 실습
R에는 신경망 모형을 이용하기 위한 package로 nnet과 neuralnet이라는 패키지가 있다. 이를 활용한 실습을 진행하여보자.
1) iris 데이터를 통한 실습 - nnet활용
## 신경망 라이브러리
install.packages("nnet")
library(nnet)
## 신경망 모형 생성
nn.iris <- nnet(Species~., data=iris, size=2, rang=0.1, decay=5e-4, maxit=200)
신경망 모형의 적합 과정이다. Species를 예측하는 것이며 3종류가 존재한다, 다른 함수들의 인수를 알아보자면,
1.size : hidden node 개수
2. maxit : 최대반복횟수
3. decay : overfitting을 피하기 위해 사용하는 weight decay parameter
4. rang : 초기 랜덤 가중치. weights on [-rang, rang]. 기본값 = 0.5
과 같다. 즉 위의 경우는 hidden layer의 노드 수를 2개로 지정하여 4(입력)-2(은닉)-3(출력)의 신경망이 구성되었다. 그리고 반복횟수는 150회 가량 진행되었다.
## 연결선과 방향의 가중치
summary(nn.iris)
위를 보면 nnet의 기본적인 activation function이 softmax를 사용한 것을 볼 수 있다. 그리고 4-2-3구조의 layer와 노드 관계를 갖고 해당 노드들에서 가중치를 확인할 수 있다.
## nnet 신경망 시각화
install.packages("devtools")
library(devtools)
source('https://gist.githubusercontent.com/fawda123/7471137/raw/466c1474d0a505ff044412703516c34f1a4684a5/nnet_plot_update.r')
plot.nnet(nn.iris)

위는 신경망 모형을 가중치에 따라 시각화 작업을 진행한 것이다. source함수는 url을 통해 github의 시각화 코드를 다운로드한 것인데, R 내부에 저장되어있는 source()함수를 사용하였다. 만약 reshape 라이브러리를 이용한다면 동일한 방식으로 source_url()함수를 사용하면 된다.
## 신경망 모형 정오분류표(confusion_matrix)
table(iris$Species, predict(nn.iris, iris, type="class"))

위의 table함수를 통해 target데이터와 predict 데이터를 비교할 수 있다. 위를 보면 setosa의 경우는 train데이터에 대한 학습결과로 모두 범주를 분류해냈지만, versicolor와 virginica는 1개의 오분류가 발생했다.
2) infert 데이터를 통한 실습 - neuralnet활용과 공변량 분석
neuralnet이 nnet과 다른 가장 큰 점은 다양한 역전파 알고리즘 및 activation function과 loss function을 사용자 선택으로 제공한다는 점이다.
## 신경망 라이브러리
install.packages("neuralnet")
library(neuralnet)
## 데이터 로드
data(infert, package = "datasets")
str(infert)

데이터의 형태는 위와 같다.
## 신경망 모형 생성
net.infert <- neuralnet(case~age+parity+induced+spontaneous, data = infert, hidden = 2,
err.fct="ce", linear.output = FALSE, likelihood = TRUE)
net.infert
위에서 보면 err.fct는 loss function으로 cross entropy를 지정해준 것이다. linear.output은 논리값을 뜻하는 것으로 activation function을 사용하지 않는다면 TRUE로 입력해주어야 한다. 그리고 likelihood는 에러함수에 대한 우도함수를 지정해주는 것으로, 만약 에러 함수가 음의 로그-우도 함수가 아니면, likelihood는 TRUE 이여야 한다. 그러면 AIC, BIC계산되는 것을 기반으로 한다.
추가적인 neuralnet()함수의 인수는 아래의 코드를 통해서 확인할 수 있다.
## neuralnet 인수 확인
names(net.infert)

그리고 학습된 결과에 대한 정보는 아래 result.matrix를 통해서 확인할 수 있다.
## neuralnet을 통해 데이터 모델에 학습된 정보확인
net.infert$result.matrix

시각화는 아래와 같이 nnet보다 더 간편하게 정의된다.
## 신경망 모형 시각화
plot(net.infert)
## 원래의 데이터와 함께 적합값을 출력
out <- cbind(net.infert $ covariate, net.infert$net.result[[1]])
dimnames(out) <- list(NULL, c("age","parity","induced","spontaneous","nn-output"))
head(out)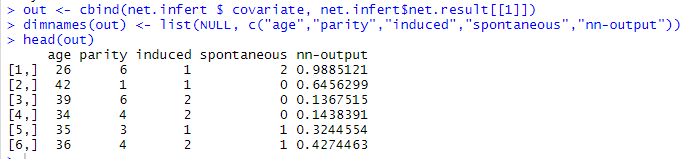
모형의 적합에 사용된 자료는 $covariate와 $response를 통해 확인이 가능하다. 그리고 적합값은 $net.result를 통해서 알 수 있다.
또한 가중치 초기설정값은 $startweights를 통해서 알 수 있으며, 적합된 가중치값은 $weights를 통해서 알 수 있다. 위 그림의 nn-output은 적합값의 출력결과와 동일하다. 앞의 age/parity/induced/spontaneous는 원데이터 값이다.
## 일반화 가중치
head(net.infert$generalized.weights[[1]])
일반화된 가중치(generalized weights)는 각 공변량들의 효과를 나타내는 것이다. 이는 로지스틱 회귀모델에서 회귀계수와 유사하게 해석된다.(각 공변량이 log-odds에 미치는 영향력을 나타내는 것이다). 그러나 로지스틱 회귀모델과는 달리 generalized weights는 모든 공변량에 의존하여 각 자료의 부분에서 국소적인 기여도를 나타낸다.
예를 들어, 동일한 변수가 어떤 변수에 대해서는 양의 영향을 가지며, 동시에 또다른 변수에 대해서는 음의 영향을 가지고 평균적으로는 0과 가까운 영향력을 가지는 것이 가능하다. 모든 자료에 대한 generalized weights은 특정 공변량의 효과가 선형적인지를 나타낸다. 즉 작은 분산은 선형효과를 제시하며, 큰 분산은 관측치 공간상에서 변화가 심하다는 뜻으로 비선형적 관계가 존재함을 말한다.
이 일반화된 가중치를 변수별로 시각화를 진행하면 아래와 같다.
## 일반화 가중치 시각화
par(mfrow = c(2,2))
gwplot(net.infert, selected.covariate = "age", min = -2.5, max = 5)
gwplot(net.infert, selected.covariate = "parity", min = -2.5, max = 5)
gwplot(net.infert, selected.covariate = "induced", min = -2.5, max = 5)
gwplot(net.infert, selected.covariate = "spontaneous", min = -2.5, max = 5)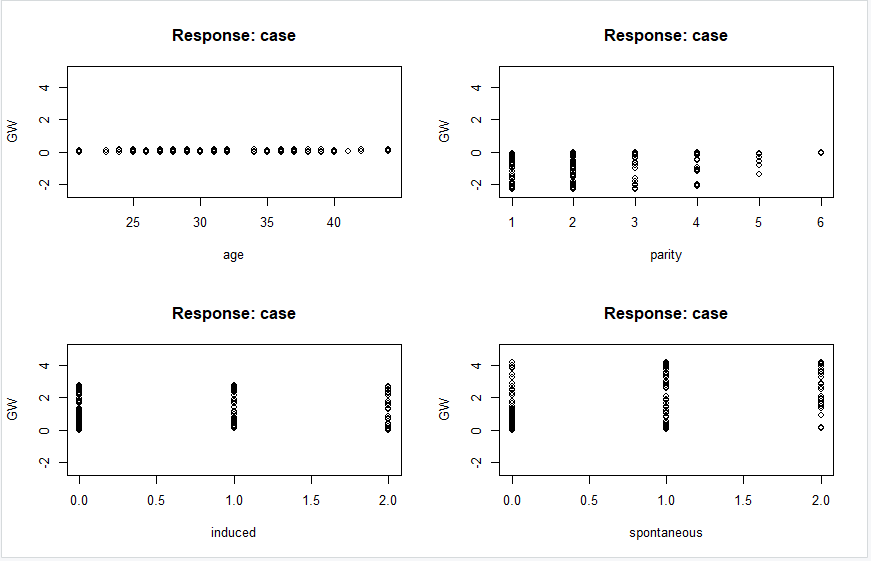
위의 일반화 가중치를 보면 age의 경우 모든 값들이 0 or 거의 0에 분포한다. 이는 결과에 미치는 영향이 없다고 볼 수 있으며, induced와 spontaneous의 경우는 전반적으로 가중치의 분산이 1보다 크기에 양의 증감관계를 갖는 비선형 효과를 갖는다고 볼 수 있다. 반대로 parity의 경우는 음으로 분포해있기에, 음의 증감관계를 갖는다고 볼 수 있다. 그렇기에 모형의 단순화를 위해서 공변량이 존재하지 않는(영향력이 없는) age변수를 제외하고 신경망 모형을 다시 적합할 수 있다.
이상 기본적인 신경망모형과 공변량에 대해서 알아보았다. 아래는 신경망 내부에서 각 뉴런의 출력값을 계산해준다. 그리고 특정 결측 공변량 조합에 대한 예측값도 구할 수 있다.
## 새로운 공변량 조합에 대한 뉴런의 output(예측결과)
new.output <- compute(net.infert, covariate = matrix(c(22,1,0,0,
22,1,1,0,
22,1,0,1,
22,1,1,1),
byrow = TRUE, ncol = 4))
new.output$net.result
위 코드는 age = 22 / parity = 1 / induced <= 1 / spontaneous <= 1을 가지는 결측 공변량 조합에 대한 예측 코드이다. 위 결과를 보면 낙태수가 증가함에 따라서(변수가 값이 발생함에 따라) 예측 확률이 증가함을 보여준다.
여태까지 hidden layer가 1개인 단층 신경망에 대해서 알아보았다. 이제 다른 예제를 통해 multi layer perceptron(다층신경망)에 대해서 알아보자. 실습데이터는 임의로 직접 만들어서 실습을 진행하겠다.
3) 다층신경망(multi layer perceptron 실습)
## 실습용 데이터 만들기
library(neuralnet) # 신경망 모형을 위한 라이브러리
train.input <- as.data.frame(runif(50,min=0,max=100))
train.output <- sqrt(train.input) # target이 input의 제곱근형태
train.data <- cbind(train.input, train.output)
colnames(train.data) <- c("Input","Output")
head(train.data)
위와 같이 실습용으로 임시 데이터를 만들었다. target은 train의 제곱근 형태이다.
## 신경망 모형 적용
net.sqrt <- neuralnet(Output~Input, train.data, hidden = 10, threshold = 0.01)
print(net.sqrt) # 모델 세부사항 모두 출력
위의 경우는 10개의 노드가 존재하는 hidden layer가 한 개인 신경망 구조이다. 위의 신경망 모형 정의 코드의 threshold= 인수는 오차함수의 편미분에 대한 값으로 정지규칙(stopping rule)으로 사용된다.
## test데이터로 예측 확인
test.data <- as.data.frame((1:10)^2)
test.out <- compute(net.sqrt, test.data)
print(test.out$net.result)
테스트 데이터를 1~10까지 제곱형태로 만들었다. 이를 예측하면 1~10에 가까운 수가 출력되어야한다. 실제로 예측 결과값이 1~10과 비슷하게 출력된다.
이제 은닉층이 2개인 모형을 적용해보자. hidden = c( a , b , c )를 통해서 벡터를 넣으면 1번 hidden에 a개 노드, 2번 hidden에 b개 노드, 3번 hidden에 c개 노드를 갖는 신경망이 만들어진다. 2개의 hidden layer만 만들어보자.
## 2개 hidden layer를 갖는 신경망 모형
net2.sqrt <- neuralnet(Output~Input, train.data, hidden = c(10,8), threshold = 0.01)
print(net2.sqrt)
plot(net2.sqrt)
위의 결과를 보면 2개의 hidden layer가 생성되었으며 각각 10/8개의 노드를 갖는 것을 확인할 수 있다.
## 2개 hidden layer를 갖는 신경망 모형의 test데이터 예측
test2.out <- compute(net2.sqrt, test.data)
print(test2.out$net.result)
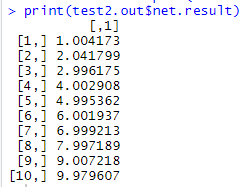
이것은 동일한 (1~10)^2 test데이터를 2개의 은닉층을 갖는 신경망으로 예측한 결과이다. 데이터 셋이 너무 단순해서 앞의 1개의 은닉층을 갖는 신경망에 비해 성능이 좋다고 단정할 수 없다. 이러한 경우는 오히려 과적합만 발생시킬 가능성이 높아진다.
결과적으로 정리하면, 신경망 모형은 변수가 많거나, input과 output의 관계가 복잡한 비선형관계가 존재할 때 유용하게 쓰일 수 있으며, 잡음에 대해서도 민감하게 반응하지 않는다. 하지만 해석이 어려운 단점이 존재한다. 그리고 은닉층의 개수와 은닉노드의 개수 또한 결정하기가 쉽지않다. 게다가 학습결과가 최적화된 global minimum loss를 발견한 것이 아니라 local minimum loss를 발견한 경우일 수도 있는데 이를 판별하기가 쉽지않은 단점이 있따. 게다가 모형이 복잡해질수록 시간이 많이 소요될 가능성이 높아진다.
이상으로 R을 활용하여 신경망 모형을 구현해보는 실습시간을 가져봤다. Python의 sklearn을 통해서 쉽게 구현하는 게시글도 이전에 작성하였다. 아래 링크를 남겨놓았으니, 관심이 있다면 한 번 봐보길 바란다.
https://todayisbetterthanyesterday.tistory.com/41
[Python] sklearn을 활용한 인공신경망(Artificial Neural Network) 모형 실습
*아래 학습은 Fastcampus의 "머신러닝 A-Z까지"라는 인터넷 강의에서 실습한 내용을 복습하며 학습과정을 공유하고자 복기한 내용입니다. 이 게시글은 오로지 파이썬을 통한 실습만을 진행한다. ��
todayisbetterthanyesterday.tistory.com
'ADP | ADsP with R > Knowledge' 카테고리의 다른 글
| [ADP] R로 하는 Ensemble(앙상블)모형 - Bagging, Boosting, RandomForest (0) | 2020.08.02 |
|---|---|
| [ADP] R로 하는 의사결정나무(Decision Tree) 모형 (1) | 2020.07.24 |
| [ADP] R로 하는 로지스틱 회귀분석 (0) | 2020.07.20 |
| [ADP] R로 하는 시계열 분석 실습(분해시계열, ARIMA) (0) | 2020.07.18 |
| [ADP] R을 활용한 다변량 분석 -상관분석/ 다차원 척도법 / 주성분분석 (PCA) (0) | 2020.07.17 |