2020. 7. 20. 17:43ㆍADP | ADsP with R/Knowledge
1. 로지스틱 회귀모형의 이해
로지스틱 회귀모형은 반응변수가 범주형인 경우( 0 or 1 ) 적용하는 회귀분석 모형이다. 로지스틱 회귀모형은 설명변수의 값이 주어질 때, 특정 종속변수 집단에 속할 확률을 추정하여 특정 임계값을 설정하여 분류작업으로 진행되기도 한다. 이 때 모형 적합을 통해 추정된 확률은 "사후확률(posterior probability)"이라고 부르기도 한다.
기본적인 다중 로지스틱 회귀모형의 수식은 아래와 같다. 아래의 식은 승산비(odds)로 표현된 것이다. 그렇기에 해석에 있어서 단순 확률이라고 읽으면 안된다. 승산비란 성공확률(주류) = p /실패확률(비주류) = (1-p)이다.
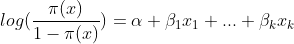
위 식에서 파이는 아래의 정의와 같다. 이를 뜻하는 것은 파이(x)란 특정 x변수에서 성공할 확률인 것이다.
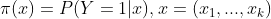
그리고 pi는 다시 로지스틱함수 형태로 변환될 수 있다.
1. 아래는 로지스틱 함수 형태로 변환된 것이다. 이를 그래프로 도식화한다면 beta1 > 0 일 경우 0부터 1사이값을 갖는 S자 모형이고 beta1 < 0 이라면 0 부터 1사이 값을 갖는 역S자 모형이다.
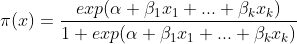
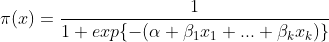
2. 이 pi표시에는 다른 의미가 한 가지 더 존재한다. 표준 로지스틱 분포의 누적함수를 F(x)라 할 때, 아래처럼 표현되며,

이는 표준로지스틱 분포의 누적분포함수로 성공의 확률을 추정한다는 것이다.
로지스틱 회귀모형 수식에 담겨있는 수학적 의미를 알아보았다. 이는 연속적인 값으로 pi값이 도출되지만, thresholde(임계값)을 설정하여 분류기로 사용할 수 있다. 그리고 threshold에는 정확도/민감도/특이도 등 여러 기준으로 로지스틱 회귀모형과 기존에 알고 있는 정보를 동시에 고려할 수도 있다.
2. R로 하는 로지스틱 회귀모형 실습 - 1
실습을 위한 데이터셋(iris) - iris 데이터는 종속변수(target)이 3개인 데이터지만, 이진형으로 실습을 진행하기 위해 데이터의 setosa와 versicolor 부분만 가져오기로 하자.
data(iris)
a <- subset(iris, Species == "setosa" | Species == "versicolor")
a$Species <- factor(a$Species)
str(a)

위에서 Species를 Factor형(범주형)으로 setosa = 1 / versicolor = 2로 인식하도록 만들었다. R에서 로지스틱을 적용할 시에는 높은 숫자의 범주를 모형화하므로 해석에 있어서 유의할 필요가 있다.
로지스틱 회귀 전, 탐색적 분석 - cdplot()
cdplot(Species~Sepla.Length, data =a )
cdplot함수는 연속형 변수의 변화에 따라 범주형 변수의 조건부 분포를 보여준다. 위의 그림은 Sepal.Length가 커짐에 따라서 versicolor의 확률이 증가함을 보여준다.
glm() 로지스틱 회귀모형 함수
b <- glm(Species~Sepal.Length, data = a, family = binomial)
summary(b)
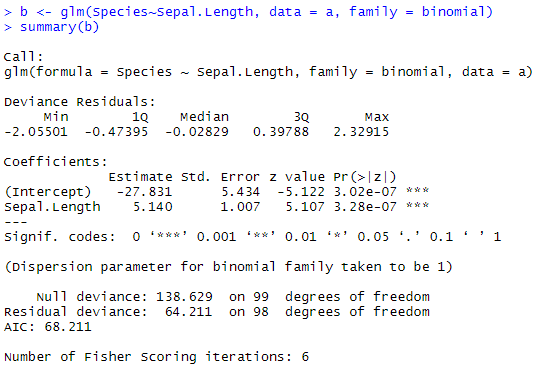
glm함수를 사용하여 로지스틱 회귀모형을 진행했다. 이를 보면 Sepal.Length의 p값이 거의 0에 가깝게 나와 매우 유의미한 변수라는 것을 확인할 수 있다. Estimate를 보면 Sepal.Length가 한 단위 증가함에 따라, odds가 exp(5.14)배 증가하는 것을 확인할 수 있다. Null deviance(절편만 포함하는 모형)와 Residual deviance(Sepal.Length변수를 사용)를 비교해볼 때, 이탈도가 74가량 감소한 것으로 보아 Sepal.Length가 영향력이 충분히 있는 변수라고 판단된다.
이탈도를 확인하는 검정기법으로 Anova검정이 있다. 이를 사용하여도 동일한 결과가 나온다.
anova(b, test="Chisq")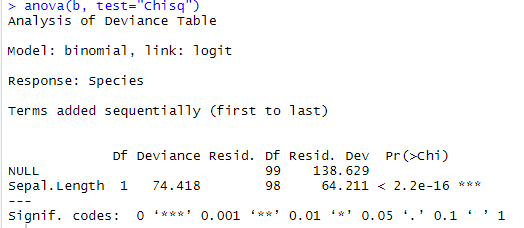
계수확인
coef(b)
exp(coef(b)["Sepal.Length"])
회귀계수 beta와 exp(beta)의 신뢰구간
confint(b,parm = "Sepal.Length")
exp(confint(b,parm = "Sepal.Length"))

위의 Sepal.Length의 계수와 신뢰구간을 확인해 보자. 신뢰구간 안에 Sepal.Length의 beta/exp(beta)가 포함됨을 확인할 수 있다. 즉 유의미한 변수라는 것이다.
로지스틱 회귀모형 적합 결과를 확인
fitted(b) 
새로운 자료 예측 - 여기선 편의상 학습데이터 "a"중 1,50,51,100번째를 그대로 사용하였다.
predict(b, newdata = a [c(1,50,51,100), ], type = "response")

적합한 로지스틱 회귀모형 그래프
plot(a$Sepal.Length, a$Species, xlab = "Sepal.Length")
x = seq(min(a$Sepal.Length), max(a$Sepal.Length), 0.1)
lines(x, 1+(1/(1+(1/exp(-27.831+5.140*x)))),type = "l", col = "Red")

데이터의 범주형 산점도에 logit에 관한 식을 line으로 표시해주었다. 로지스틱 회귀분석은 위와같은 형태로 도식화된다.
이상 변수가 1개일 경우의 로지스틱 회귀모형에 대해서 알아보았다. 사실 변수가 추가되더라도 작업하는 과정은 동일하다. 단지 학습 및 검정을 진행할 때 target ~ col1 + col2 ... 식으로 모델에 학습할 인수만 바꿔주면 되는 것이다.
'ADP | ADsP with R > Knowledge' 카테고리의 다른 글
| [ADP] R로 하는 의사결정나무(Decision Tree) 모형 (1) | 2020.07.24 |
|---|---|
| [ADP] R로 하는 신경망(Neural Network) 모형 (0) | 2020.07.24 |
| [ADP] R로 하는 시계열 분석 실습(분해시계열, ARIMA) (0) | 2020.07.18 |
| [ADP] R을 활용한 다변량 분석 -상관분석/ 다차원 척도법 / 주성분분석 (PCA) (0) | 2020.07.17 |
| [ADP] R을 활용한 변수 선택법 ( step()함수 - Forward, Backward, Stepwise ) (0) | 2020.07.17 |