2020. 7. 17. 19:20ㆍADP | ADsP with R/Knowledge
1. 상관 분석
상관분석은 데이터에 존재하는 두 변수 간의 관계를 알아보기 위해서 진행한다. 즉, 상관계수를 알아보는 것이다. 두 변수간의 상관관계를 측정하는 상관계수는 피어슨 상관계수와 스피어만 상관계수가 있다.
1) 피어슨 상관계수
피어슨 상관계수의 수식은 아래와 같다. 이때 상관계수는 -1<= p <= 1 이고, X와 Y가 독립이면 p = 0이다.

모수인 피어슨 상관계수를 추정하기 위해서는 표본상관계수 r을 사용하며 수식은 아래와 같다.

2) 스피어만 상관계수
피어슨 상관계수는 두 변수간 선형관계의 크기를 측정하는 값이기에, 비선형 관계의 상관관계는 나타내지 못한다.
반면 스피어만 상관계수는 단조증가함수로 변환하여 비선형적인 관계 또한 나타낸다. 스피어만 상관계수는 두 변수를 모두 순위로 변환시켜, 두 변수의 순위 사이의 피어슨 상관계수를 구하는 것이다.
스피어만 상관계수의 수식은 아래와 같다.

3)상관계수를 R을 활용하여 알아보는 실습을 진행해보자.
3-1) 피어슨 상관계수 실습
# 피어슨/스피어만 상관계수 구하기 위한 라이브러리 Hmisc 설치 및 로드
install.packages("Hmisc")
library(Hmisc) data(mtcars)
head(mtcars)
# 두 변수간의 산점도, 직선관계
drat <- mtcars$drat
disp <- mtcars$disp
plot(drat, disp)

# 두 변수간의 상관관계 = 피어슨 상관계수
cor(drat, disp)

여기까지 두 변수간의 산점도와 상관관계를 확인해보았다. 기본적으로 R에 내장된 함수인 cor은 피어슨 상관계수를 구해주는 함수이다. 그렇기에 스피어만 상관계수를 알기 위해서는 추가적인 패키지 설치가 요구된다.
우리가 설치하고 로드한 "Hmisc"패키지에는 rcorr함수를 이용해서 데이터셋 전체의 상관관계를 한 번에 알아볼 수 있다.
# 전체 변수들간의 피어슨 상관계수 + 귀무가설에 대한 p-value출력
rcorr(as.matrix(mtcars), type = "pearson")

위의 결과표를 보면 첫 번째 수치 데이터는 피어슨 상관관계를 나타낸 것이고, 두 번째 수치 데이터는 귀무가설 H0 = 0 에 대한 p-value를 나타낸 것이다.
아래는 공분산이다. 상관계수와 밀접한 관련이 있다.
# 두 변수간의 공분산 Cov(X,Y)
cov(drat, disp)

3-2) 스피어만 상관계수 실습
# 전체 변수들간의 스피어만 상관계수 + 귀무가설에 대한 p-value출력
rcorr(as.matrix(mtcars), type = "spearman")

위의 결과표를 보면 첫 번째 수치 데이터는 스피어만 상관관계를 나타낸 것이고, 두 번째 수치 데이터는 귀무가설 H0 = 0 에 대한 p-value를 나타낸 것이다.
2. 다차원 척도법
다차원 척도법은 여러 대상 간의 거리가 주어졌을때, 대상들을 동일한 상대적 거리를 가진 실수공간의 점들로 배치시키는 방법을 말한다. 거리의 경우 추상적일 수도 있고 실수공간에서의 거리가 될 수도 있다.
그렇기에 다차원 척도법은 주로 자료들의 상대적인 관계를 이해하는 시각화방법의 근간으로 이용된다.
간단한 실습을 통해서 다차원 척도법을 알아보자.
# 유로 거리(distance) 데이터
data(eurodist)
eurodist
eurodist는 유럽의 도시 사이 거리를 매핑한 자료이다
# cmdscale을 사용하여 각 도시의 상대적 위치를 도식화 할 수 있는 X,Y좌표계산
loc <- cmdscale(eurodist)
loc
cmdscale을 사용하여 각 도시간의 상대적 위치를 도식화할 X,Y좌표를 생성했다. [,1] [,2]가 나타내는 것이 X,Y좌표이다.
# plot을 통한 시각화
x <- loc[,1]
y <- loc[,2]
plot(x,y,type = "n", main = "eurodist")
text(x,y,rownames(loc),cex = 0.8)
abline(v=0,h=0)

cmdscale을 통한 상대적 위치를 plot을 통하여 도식화하였다.
이러한 식으로 다차원 척도법을 진행할 수 있다. 물론 이 방법은 3차원 그래프에서도 동일하게 적용시킬 수 있다.
3. 주성분 분석
주성분 분석은 python을 통해서 또한 게시물과 예제에서 다루었다. 이 게시글에서는 R을 이용한 주성분분석의 실습과정만 진행하겠다.
1. 주성분 분석의 상세한 원리와 이해는 아래 링크를 통해서 학습하면 된다.
https://todayisbetterthanyesterday.tistory.com/22?category=822147
[Data Analysis 개념] 차원 축소법 - PCA(주성분 분석)
이 게시글은 PCA의 이해와 수학적 과정만을 다룬다. Python 실습코드를 따라가보면 훨씬 이해가 잘 될 것이다. 아래 링크를 남겨놓겠다. https://todayisbetterthanyesterday.tistory.com/16 [Python] - PCA(주..
todayisbetterthanyesterday.tistory.com
2. 주성분 분석의 Python 구현 실습
https://todayisbetterthanyesterday.tistory.com/16?category=821465
[Python] - PCA(주성분분석) 실습
*아래 학습은 Fastcampus의 "머신러닝 A-Z까지"라는 인터넷 강의에서 실습한 내용을 복습하며 학습과정을 공유하고자 복기한 내용입니다. PCA는 Principal component analysis의 약자로 차원의 저주를 해결�
todayisbetterthanyesterday.tistory.com
R을 활용하여 실습을 진행해보자.
# dataset 로드
library(datasets)
data(USArrests)
summary(USArrests)
기존 변수들에 대한 사분위수, 평균값이다.
# 주성분분석 (PCA) fitting
fit <- princomp(USArrests, cor = TRUE)
summary(fit)

princomp함수를 사용하여 PCA를 진행하였다. cor = TRUE 옵션을 주어 주성분분석을 공분산 행렬이 아닌 상관계수 행렬을 사용하여 fitting을 시켰다. summary(fit)의 결과는 4개의 PC에 대한 표준편차, 분산의 비율 등을 보여준다. 예를 들어 1번째 PC 하나가 전체 데이터의 62퍼센트를 설명한다는 이야기이다. 두 번째 PC까지만 사용하여 대략 87퍼센트의 데이터를 설명할 수 있다.
이처럼 주성분 분석은 차원이 많은 경우 데이터 손실을 최소화하면서 차원을 줄일 수 있다.
# 주성분 PC들의 로딩벡터
loadings(fit)
이를 통해서 첫번째와 두번째 주성분이
Y1 = 0.536murder + 0.583assault + 0.278ubanpop + 0.543rape
Y2 = 0.418murder + 0.188assault - 0.873urbanpop - 0.167rape
으로 주어지는 것을 확인할 수 있다.
# scree plot - 주성분의 분산 plot
plot(fit, type = "lines")
위의 그래프를 통해서 기울기가 급격히 완만해지는 지점까지 PC를 선택하는 것도 PCA에서 주성분의 개수를 선택하는 방법중 하나이다. 그리고 총 분산의 비율이 70~90%를 차지하는 지점까지 PC를 선택하는 방법도 있다.
# 모든 관측치/변수를 주성분으로 표현
fit$scores
fit$scores는 각 관측치를 주성분들로 표현한 값들을 나타낸다.
# 첫 번째와 두 번째 주성분의 좌표에 관측치들을 그린 plot
biplot(fit)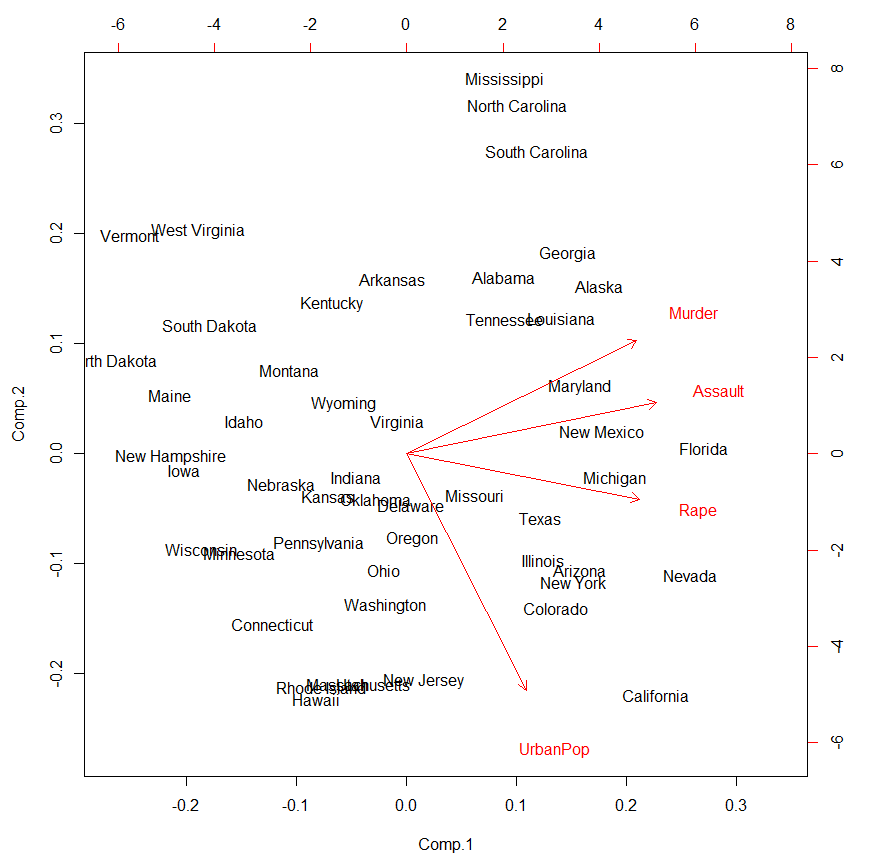
관측치들을 첫 번째와 두 번째 주성분의 좌표에 그린 것이다. 첫 번째 주성분이 Assault, Murder, Rape와 비슷한 방향을 가진다. 그렇기에 이러한 변수에 대한 가중치가 높게 적용된 것이다. 두 번째 주성분은 urban pop과 상대적으로 평행하기에 urban pop에 큰 영향을 받았을 것이다.
이상 R을 통한 다변량 분석을 진행해 보았다.
'ADP | ADsP with R > Knowledge' 카테고리의 다른 글
| [ADP] R로 하는 로지스틱 회귀분석 (0) | 2020.07.20 |
|---|---|
| [ADP] R로 하는 시계열 분석 실습(분해시계열, ARIMA) (0) | 2020.07.18 |
| [ADP] R을 활용한 변수 선택법 ( step()함수 - Forward, Backward, Stepwise ) (0) | 2020.07.17 |
| [ADP] R을 활용한 단순회귀/다중회귀/다항회귀분석 실습 (0) | 2020.07.16 |
| [ADP] R - 결측값 처리와 이상값 탐색 (0) | 2020.07.14 |