2020. 7. 2. 17:29ㆍML in Python/Knowledge
※ 이 게시글은 나이브 베이즈 분류에 대한 이론만 게시된 게시글입니다. 만약 파이썬을 통한 구현에서만 알아보고 싶다면 아래 링크를 통해 실습과정을 확인해주시면 됩니다.
https://todayisbetterthanyesterday.tistory.com/18?category=821465
[Python] Gaussian/Multinomial Naive Bayes Classification(가우시안/다항 나이브 베이즈 분류) 실습
*아래 학습은 Fastcampus의 "머신러닝 A-Z까지"라는 인터넷 강의에서 실습한 내용을 복습하며 학습과정을 공유하고자 복기한 내용입니다. 나이브 베이즈 모델은 데이터가 적을 때, 간단한 학습으��
todayisbetterthanyesterday.tistory.com
나이브 베이즈 분류 예시) 테니스를 좋아하는 한 사람이 있다고 하자. 만약, 이 사람이 1. 날씨가 좋고 2. 습도가 낮은 날에 테니스를 칠 확률은 얼마나 되는가?
주어진 데이터에 따라 경우가 다르겠지만, "1. 이 사람이 테니스를 많이 칠 수록, 2. 테니스를 쳤을 때, 해당 날씨가 좋고 습도가 낮은 경우가 많을 때"일수록 이 사람이 날씨가 좋고 습도가 낮은 날에 테니스를 칠 확률이 높아진다.
조건부 확률
이를 수학적 개념을 통해 알아보자.
먼저, 조건부 확률에 대해서 알 필요가 있다. 이해하기 쉽도록 "B가 주어졌을 때 사건 A의 조건부 확률"은 아래와 같다.

이는 B사건 중에서 A사건이 동시에 발생한 경우를 나타낸다.
즉, 위의 예시에서 좋은 날씨와 낮은 습도가 고정되어 있을 때, 테니스를 칠 조건부 확률이 올라가면, 저 경우의 확률이 올라간다.
베이즈 정리
이제 약간 더 나아가 보자.
베이즈 정리의 정의는 "A1,...,Ak가 배반사건이고, A1,...Ak의 합집합이 전체 집합(=S)일 때,

를 만족하는 것이다.
테니스 예시에 적용

이는 날씨가 좋고, 습도가 낮을 때, 테니스를 칠 확률과 안 칠 확률 분에 동일 조건 하에서 테니스를 칠 확률이다. 결국 날씨가 좋고, 습도가 낮을 경우에 얼마나 테니스를 쳤느냐가 된다.

사실 여태 계속 같은 말을 반복했다. 이를 수식으로 풀어써서 그렇다. 결국 베이즈 정리는 직관적인 경우를 수치화하여, 알고리즘으로 구현한 것이다. 이것이 바로 "나이브 베이즈 분류"의 원리이다.
나이브 베이즈의 종류와 이해
나이브 베이즈 분류에는 대표적으로 2가지 경우가 있다.
1. 설명변수가 연속형 변수일 때, Gaussian Naive Bayes (가우시안 나이브 베이즈)
2. 설명변수가 범주형 변수일 때, Multinomial Naive Bayes (다항 나이브 베이즈)
그리고 같은 범주형 변수일 때, 범주가 2개밖에 없는 이진형일 경우 Bernoulli naive Bayes (베르누이 나이브 베이즈)로 분류된다. 사실 베르누이 나이브 베이즈는 다항 나이브 베이즈와 같은 형태인 셈이다.
Gaussian Naive Bayes
가우시안 나이브 베이즈는 표본 평균과 표본 분산을 가진 정규분포 하에서 베이즈 정리를 사용한 것이다.
1.

즉, y의 범주가 정해져 있을 때
2.

y=c에서 X=x의 정규분포의 표현식은 위와 같이 된다.
3.

이를 위와 같이 조건부 독립으로 표현하면
4.

등식의 우측항의 분모는 항상 같은 조건을 나타내는 집합이기에, 분류 모델의 선택편의를 위해 분자만 비교를 하고자 한다. (3)과 (4)는 같은 식은 아니지만, 항상 동일한 조건인 분모만 제외시킨 식이 된다.
5.

이 경우, 조건부독립에 정규분포를 대입해주면 위와 같은 최종식이 도출된다.
이것이 바로 Gaussian Naive Bayes이다. 즉, 정규분포를 가정한 표본들을 대상으로 조건부 독립을 나타내, 항상 같은 분모를 갖는 조건하에서, 분자의 값이 가장 큰 경우,즉 확률이 가장 높은 경우를 "선택"하는 것이다.
Multinomial Naive Bayes
1.

y와 k의 범주가 정해져 있을 때,
2.

y=c인 상황에서, Xk가 xk일 조건부 확률은, 즉 범주 small k 가 출현한 횟수는
- 각각의 출현한 횟수를 모두 곱한 것 분의 각각의 출현한 횟수를 다 더한 것의 팩토리얼 -> 같은 것이 있는 순열 식
- 각각의 범주 출현 확률에 xk번 출현하여 xk번 곱해주는 것이다.
Bernoulli naive bayes
1.

두 가지 범주가 주어져 있을 때, 출현할 확률은 쪼개질 수 있고,
2.

조건부 확률은 다항분포 (베르누이 정리/이항정리)로 표시될 수 있으며
3.

좌항과 우항이 사실 같지는 않지만, 분모는 항상 동일한 조건을 띄기에 무시하고
4.
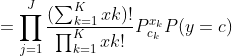
다항분포를 사용한 범주형 조건부 확률을 구할 수 있게 된다.
'ML in Python > Knowledge' 카테고리의 다른 글
| [Data Analysis 개념] k-Fold Cross Validation (0) | 2020.07.03 |
|---|---|
| [Data Analysis 개념] KNN(K-Nearest-Neighbors)알고리즘 (0) | 2020.07.03 |
| [Data Analysis 개념] 차원의 저주 (0) | 2020.06.25 |
| 회귀계수 축소법 - Lasso, Ridge, Elastic-Net 개념 (0) | 2020.06.23 |
| 헷갈리는 통계기본 - 정확도, 정밀도, 재현율, 특이도, G-mean, F1 measure, ROC curve&AUC, Gain Chart & Lift curve 정리 (2) | 2020.06.09 |