2020. 6. 9. 15:05ㆍML in Python/Knowledge
추출한 훈련용 자료를 사용하여 분류 모형을 적합후 검증용 데이터를 사용하여 정확도를 평가할 때, 범주형 변수에 대해 사용되는 confusion matrix, ROC curve, gain chart, lift curve에 대해서 알아보자.
모델 성능 평가 방법
1. Confusion matrix(오분류표)
오분류표는 아래의 형태와 같다.

TP(True Positive) : 실제값과 예측치 모두 True
TN(True Negative) : 실제값과 예측치 모두 False
FP(False Positive) : 실제값은 False, 예측은 True
FN(False Negative) : 실제값은 True, 예측은 False
로 이루어진 표이다.
이 때
정분류율(accuracy) = TP + TN / TP + FN + FP + TN
이는 전체 관측치 중 실제값과 예측치가 일치한 정도를 나타낸다. 정분류율은 범주의 분포가 균형을 이룰 때 효과적인 평가지표이다.
오분류율(error rate) = FP + FN / TP + FN + FP + TN
모형이 제대로 예측하지 못한 관측치를 평가하는 지표이다. 이는 1-accuracy와 동일하다.
민감도(sensitivity) = TP / TP + FN
범주 불균형 문제를 갖고있는 데이터에 대한 분류분석 모형의 평가지표는 중요한 분류 범주만 다루어야 한다. 이때 사용되는 지표가 민감도와 특이도이다. 민감도는 실제값이 True인 경우 예측치가 적중한 정도를 나타낸다.
특이도(specificity) = TN / FP + TN
범주 불균형 문제를 갖고있는 데이터에 대한 분류분석 모형의 평가지표는 중요한 분류 범주만 다루어야 한다. 이때 사용되는 지표가 민감도와 특이도이다. 특이도는 실제값이 False인 관측치중 예측치가 적중한 정도를 나타낸다.
정확도(Precision) = TP / TP + FP
정확도는 True로 예측한 관측치중 실제값이 True인 정도를 나타내는 정확성 지표이다.
재현율(Recall) = TP / TP + FN
재현율은 실제값이 True인 관측치 중에서 예측치가 적중한 정도를 나타내는 민감도와 동일한 지표로 모형의 완정성을 나타낸다.
위와 같이 정확도와 재현율은 모형의 평가에 대표적으로 사용되는 지표이긴 하지만, 한 지표값이 높아지면 다른 지표의 값이 낮아질 가능성이 높은 관계를 갖고있다. 암환자를 예를 들어보자. 암환자의 분류 분석 모형에서 대부분의 사람을 암환자로 예측한다면, 높은 정확도를 가지게 되겠지만, 재현율은 현저하게 낮아질 것이다. 이러한 효과를 보정하기 위한 것이 바로 F1 score와 F_beta지표이다.
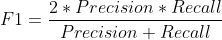
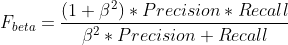
F1 score는 정확도와 재현율의 조화평균을 나타내며, 정확도와 재현율에 동일한 가중치를 부여하여 평균을 낸다. F_bet지표는 양수 beta값만큼을 재현율에 가중치를 주어 평균을 낸다. 예를들어 F_2는 재현율에 정확도의 2배만큼 가중치를 부여하고 F_0.5의 경우 정확도에 2배의 가중치를 부여하는 것이다.

그리고 G-mean의 경우도 있다. 이때는 제 1종 오류와 제 2종 오류 중 성능이 더 나쁜쪽에 가중치를 주는 방식이다.
2. ROC curve
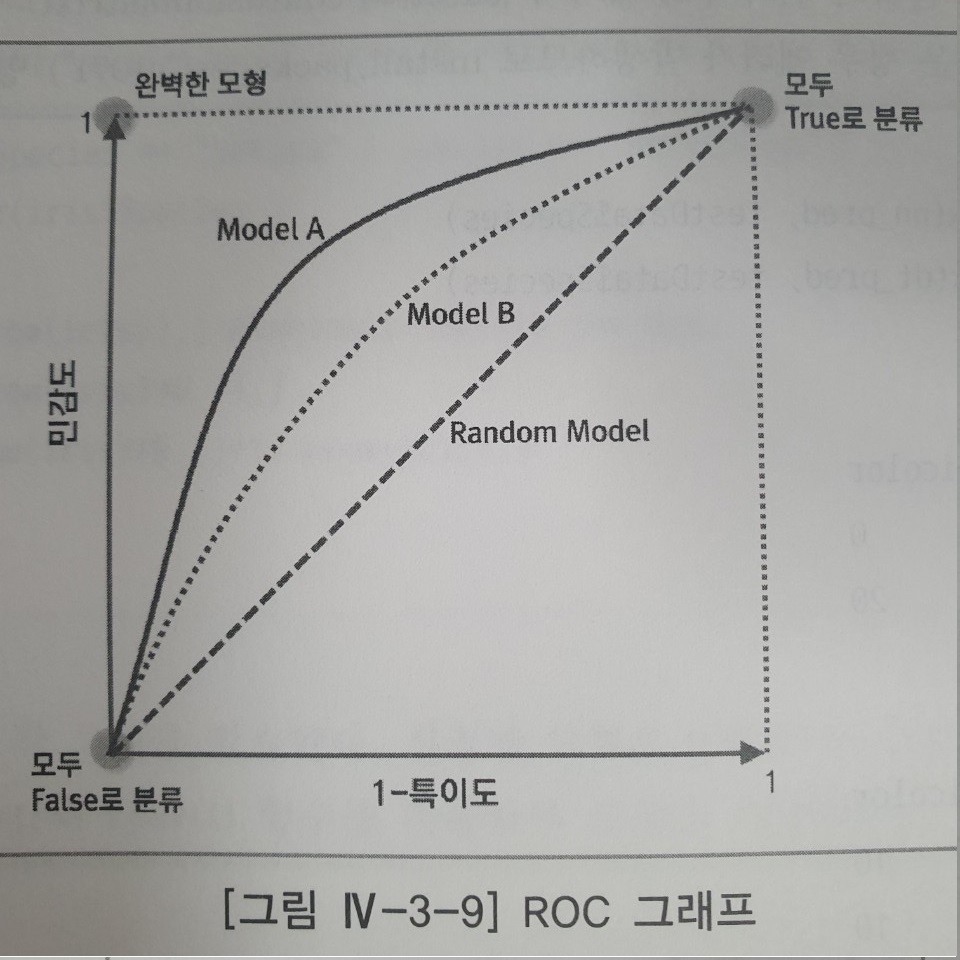
위의 이미지는 한국 데이터산업진흥원에서 편찬한 "데이터 분석 전문가 가이드"책에서 가져온 것이다. 이 이미지가 넷상 다른 이미지보다 설명을 잘 하기에 가져왔다. ROC(Receiver Operating Characteristic) curve는 레이더 이미지 분석의 성과를 측정하기 위해서 개발이 되었다. 두 분류 모형을 비교/분석 결과를 가시화할 수 있다는 점에서 유용하다.
ROC 그래프의 x축은 FP Ratio(1-특이도)를 나타내며, y축에는 민감도를 나타내어 이 두 평가 값을 기준으로 모형을 평가한다. 모형의 성능을 평가하는 것은 ROC curve의 밑부분의 면적이 넓을수록 좋은 모형으로 평가받는다. 위에서 보듯이 x축(1-특이도)과 y축(민감도) 모두 1인 경우는 모두 True로 분류를 한 것이고 x축과 y축 모두 0인 경우는 모두 False로 분류한 것이다. x축은 0 y축은 1의 경우가 AUC(ROC curve 아래의 면적) = 1로 가장 좋은 모형인 것이다. 즉, AUC(ROC curve 아래의 면적)가 1에 가까울수록 좋은 모형인 것이다.
위의 그림에서는 model A가 model B보다 좋은 모형인 것이다.
3. Gain Chart & Lift curve
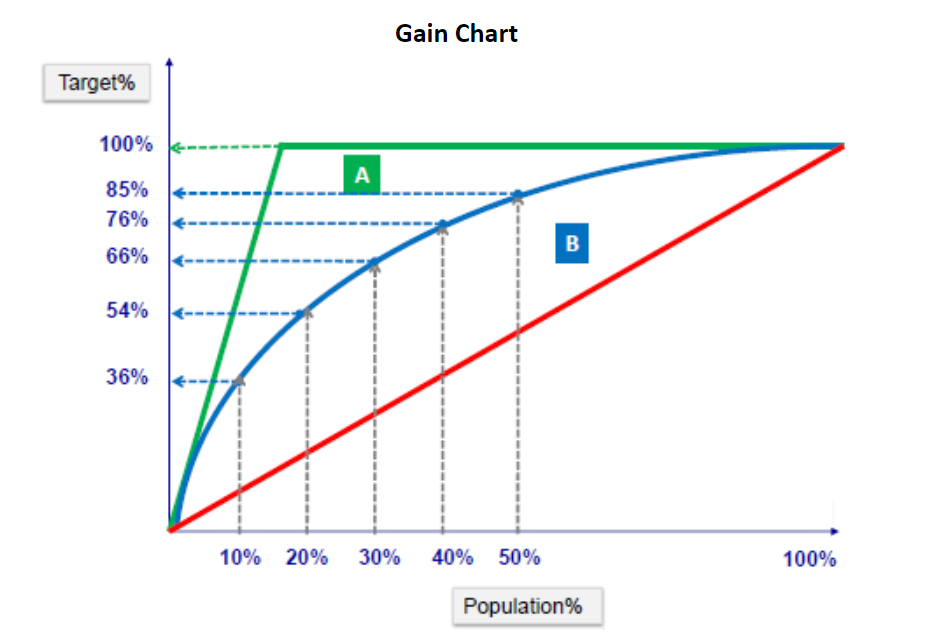
이익(Gain)은 목표 범주에 속하는 개체들이 각 등급에 얼마나 분포하고 있는지를 나타내는 값이다. 해당 등급에 따라 계산된 이익값을 누적으로 연결한 도표가 바로 Gain Chart(이익도표)이다. 즉, 분류 모형을 사용하여 분류된 관측치가 각 등급별로 얼마나 포함되는지를 나타내는 도표이다.
아래의 그림은 Gain chart이다.
Lift curve(향상도 곡선)은 랜덤 모델과 비교했을 때, 해당 모델의 성과가 얼마나 향상되었는지를 각 등급별로 파악하는 그래프이다. 상위 등급에서의 향상도가 매우 크고 하위 등급으로 갈 수록 향상도가 감소하게 되어, 일반적으로 이러한 모형의 예측력이 좋다는 것을 의미하지만, 등급에 관계없이 향상도가 차이가 없게 되면 모형의 예측력이 좋지 않음을 나타낸다.
아래의 그림이 Lift curve이다.

'ML in Python > Knowledge' 카테고리의 다른 글
| [Data Analysis 개념] KNN(K-Nearest-Neighbors)알고리즘 (0) | 2020.07.03 |
|---|---|
| [Data Analysis 개념] NaiveBayes(나이브 베이즈) 모델 - 조건부 확률 / 베이즈 정리 / Multinomial, Gaussian, Bernoulli NaiveBayes (0) | 2020.07.02 |
| [Data Analysis 개념] 차원의 저주 (0) | 2020.06.25 |
| 회귀계수 축소법 - Lasso, Ridge, Elastic-Net 개념 (0) | 2020.06.23 |
| 헷갈리는 통계기본 - 신뢰구간/신뢰도/유의수준/유의확률/검정력 (0) | 2020.06.07 |