[Python]변수선택법 실습(1) - 변수선택법 실습 이전단계, 불필요한 변수 제거 및 가변수 추가 ~ 다중공선성 확인작업 (변수선택법의 코드는 (2)에서)

 

실습에 사용될 데이터 : Toyota Corolla Data (Toyota Corolla 모델 차 가격/기능 데이터)

ToyotaCorolla.csv

0.21MB

 

 

- 이번 게시물은 변수 선택 전의 단계를 진행할 것이며, 다음 게시물에서 변수선택에 관해 논의하도록 하자 

 회귀분석을 할 때 다중공선성이 발생하면, 데이터 분석의 신뢰성이나 예측 정확도를 떨어뜨린다. 이러한 문제를 하기 위한 방법 중 하나로 데이터 선정/전처리 과정에서 "변수선택"이 매우 중요하다. 

 

변수 선택법(Variable Selection)은 

1. 전진선택법(Forward Selection)

2. 후진소거법(Backward Elimination)

3. 단계적선택법(Stepwise Selection)

이 있다.

이 변수 선택법들을 알아가기 위해 Python을 통한 실습을 진행해보자.

변수선택법을 위한 전처리 및 다중공선성 모델확인과정을 여기서 진행할 것이다. 이를 skip하고 싶다면 다음 게시글

https://todayisbetterthanyesterday.tistory.com/10

[Python]변수선택법 실습(2) - 전진선택법/후진소거법/단계적선택법/MAPE 모델 성능 평가 (변수선택��

로 바로 넘어가면 된다.

 

import pandas as pd
import numpy as np
import statsmodels.api as sm
from sklearn.model_selection import train_test_split

# 데이터 불러오기

corolla = pd.read_csv("./ToyotaCorolla.csv")
corolla.head()

corolla.head() - 0,1로 이루어진 범주형 변수가 많다.

# 데이터 수와 변수의 수 확인하기

nCar = corolla.shape[0]
nVar = corolla.shape[1]

print(nCar,nVar)                       # 1436-row , 37-col

corolla.info()

corolla.info()

 위의 corolla.info() 출력결과를 확인해보면 Model과 Fuel_Type이 각각 문자열을 이름으로 갖는 object인 것을 확인할 수 있다. 하지만, Model의 경우 자동차 모델(이름)이기에 각각의 행마다 다르고 이를 수정해 줄 필요는 없어보인다. 

# Fuel_Type 변수 확인

corolla.Fuel_Type.unique() 

corolla.Fuel_Type.unique()

 df.col.unique() 함수를 통해 데이터의 컬럼에 존재하는 명목형 변수의 중복제거된 값들을 확인해 보았다. 총 3가지 종류가 있는 것으로 확인되어 이를 데이터 분석을 위한 수치화를 진행할 필요가 있어보인다.

---

범주형 변수를 이진형 변수로 변환

# 가변수 생성

dummy_p = np.repeat(0,nCar)
dummy_c = np.repeat(0,nCar)
dummy_d = np.repeat(0,nCar)

dummy_p

dummy_p 가변수 출력물

앞에서 corolla.shape[0]을 통해 만들어 주었던 nCar을 사용하여 col개수와 같은 ndarray형태의 "0"데이터 변수를 생성했다. 이는 각각 Fuel_Type - Diesel, Petrol, CNG를 이진형 변수 ( 0 or 1 ) 로 만들어 주기 위한 가변수이다.

# boolean 인덱싱을 통해 boolean index 행렬 생성

p_idx = np.array(corolla.Fuel_Type == "Petrol")
d_idx = np.array(corolla.Fuel_Type == "Diesel")
c_idx = np.array(corolla.Fuel_Type == "CNG")

p_idx

p_idx - boolean indexing의 결과

# boolean index 행렬을 사용하여 가변수에 대입 ( True = 1, False = 0 )

dummy_p[p_idx] = 1
dummy_d[d_idx] = 1
dummy_c[c_idx] = 1

dummy_p

dummy_p - 범주형변수를 이진형으로 변환시켜준 출력물

불필요한 변수를 제거하고 가변수를 붙여주는 작업

 현재 데이터 셋에 37개의 변수(column 수)가 존재한다. 여기서 "Model"이름이나 "ID"같은 변수는 자동차의 가격에 영향을 미치는 변수가 아니라 그냥 고유 번호 및 이름을 나타내는 변수이기에 삭제한다. 그리고 새로 생성한 이진형 가변수를 붙여주기 위해 "Fuel_Type(범주형 기존변수)"를 삭제할 필요가 있다.

# 행렬로 존재하는 가변수 -> 데이터프레임으로 전환

Fuel = pd.DataFrame({"Petrol" : dummy_p, "Diesel" : dummy_d, "CNG" : dummy_c})
Fuel

새로 만든 데이터프레임 Fuel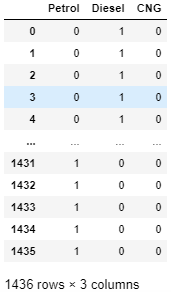

# 불필요한 변수 삭제 및 가변수 붙이기

corolla_ = corolla.drop(["id","Model","Fuel_Type"],axis = 1, inplace = False)
mlr_data = pd.concat((corolla_,Fuel),1)
mlr_data.head()

mir_data - 기존 corolla data에서 불필요한 변수가 삭제되고 뒤에 Petrol, Diesel, CNG 변수가 붙었다.

# bias를 위한 상수항 추가

mlr_data = sm.add_constant(mir_data, has_constant = "add")
mlr_data

맨 앞에 상수항을 붙인 mir_data

설명변수(X)와 타겟변수(Y)를 분리/학습데이터와 평가데이터를 분할

feature_columns = mlr_data.columns.difference(["Price"]) # Target column 빼기

X = mlr_data[feature_columns]
y = mlr_data.Price

train_x, test_x, train_y, test_y = train_test_split(X,y, train_size = 0.7, test_size = 0.3)

print(train_x.shape, test_x.shape, train_y.shape, test_y.shape)

Split Data Set Shape 출력물

# train & 회귀모델 적합

full_model = sm.OLS(train_y,train_x)
fitted_full_model = full_model.fit()

fitted_full_model.summary()

OLS모델적합 결과

 위의 R^2를 보면 0.901로 매우 높은 편이다. 그리고 이렇게 변수가 많아질 수록 변수 하나하나에 대한 신뢰도는 떨어진다. Warnings를 보면 강한 다중공선성문제가 있을 수 있다고 말하고 있다. VIF를 통해 다중공선성을 확인해보자.

# VIF를 통한 다중공선성 확인

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(mlr_data.values, i) for i in range(mlr_data.shape[1])]
vif["features"] = mlr_data.columns
vif

vif 출력물

 위의 OLS와 VIF 검정을 모두 확인했을 때, P-value가 유의하고 VIF값이 매우 높아도 논리적으로 중요한 변수라고 생각하면 변수를 지우지 않고 살릴 필요가 있다. 이러한 과정을 통해 중요하지 않은 변수 중에서, P-value가 높고 VIF값이 높은 변수를 선택해서 제거해야한다. 

# 학습데이터의 잔차 확인

res = fitted_full_model.resid

# q-q plot을 통한 잔차의 정규분포 확인
fig = sm.qqplot(res,fit = True,line = '45')

sm.qqplot(res, fit = Ture, line = '45')

 q-q plot은 잔차의 정규성을 확인할 때 쓰는 그래프 중 하나로, statsmodels.api 라이브러리 내에 존재한다. 이 q-q plot은 y=x의 형태를 띄어야 정규성을 보이는 것이다. 위의 그래프를 보면 잔차가 완전한 정규성을 보이지 않는 것을 확인할 수 있다. 하지만, 실제데이터는 잔차가 완전한 정규성을 띄는 것을 확인하기 힘들다. 보통 위의 그래프처럼 실제에서도 꼬리부분의 값을이 정규성을 띄지 않는 경우가 많다. 그래도 위의 그래프는 꼬리부분 약간의 데이터를 제외하고 정규성을 띄고 있다고 판단되어 양호하다는 판단이 가능하다.

# 잔차패턴 확인

pred_y = fitted_full_model.predict(train_x)

import matplotlib.pyplot as plt 

plt.xlim(4000,30000)
plt.xlabel('Fitted values')
plt.ylabel('Residual')

predict값과 residual의 산점도

 위의 그래프는 모든 변수를 사용해 학습된 모델의 예측값과 잔차간의 상관관계를 확인하기 위해 나타낸 산점도이다. 이를 보면 특별한 경향이 발견되지 않으므로 잔차가 균등하게 나와있다고 판단가능하다. 

# 검증데이터에 대한 예측

pred_y2 = fitted_full_model.predict(test_x)

# 예측데이터 잔차

plt.plot(np.array(test_y - pred_y2), label = "pred_full")
plt.legend()
plt.show()

예측오차 plot

 위를 보면 한가지 이상값을 제외하고 예측오차가  

#MSE 구하기

from sklearn.metrics import mean_squared_error

mean_squared_error(y_ture = test_y, y_pred = pred_y2)

MSE

 이러한 과정으로 데이터를 확인하고 변수를 제거해야하는지 확인하는 작업이 사전에 필요하다. 그리고 다중공선성/과적합 등 문제가 발생하면 변수를 가공하고, 범주형 변수는 가변수생성을 통해 추가적인 변수로 변환할 필요가 있다. 이 과정 후에 변수선택법을 적용하여 변수를 선택하고 축소하는 과정이 이어진다.  

 그렇기에 다음 게시물로는 전진선택법/후진소거법/단계적선택법의 코드와 과정을 알아보고 MAPE를 통해 변수제거한 모델의 성능평가하는 과정을 알아보도록하자