2020. 6. 13. 17:52ㆍML in Python/Python
실습에 사용될 데이터 : 보스턴 주택 데이터
Target Data
-1978 보스턴 주택 가격
-506개 타운의 주택 가격 중앙값 (단위 1,000 달러)
Feature Data
CRIM: 범죄율
INDUS: 비소매상업지역 면적 비율
NOX: 일산화질소 농도
RM: 주택당 방 수
LSTAT: 인구 중 하위 계층 비율
B: 인구 중 흑인 비율
PTRATIO: 학생/교사 비율
ZN: 25,000 평방피트를 초과 거주지역 비율
CHAS: 찰스강의 경계에 위치한 경우는 1, 아니면 0
AGE: 1940년 이전에 건축된 주택의 비율
RAD: 방사형 고속도로까지의 거리
DIS: 직업센터의 거리
TAX: 재산세율'''
import pandas as pd
import numpy as np
import statsmodels.api as sm
# 데이터 불러오기
boston = pd.read_csv("./Boston_house.csv")
boston_data = boston.drop(['Target'], axis=1)
# crim, rm, lstat을 통한 다중 선형회귀분석
x_data = boston[["CRIM","RM","LSTAT"]] #변수 여러개
target = boston[["Target"]]
# for b0, 상수항 추가
x_data1 = sm.add_constant(x_data, has_constant = "add")
# OLS 검정
multi_model = sm.OLS(target, x_data1)
fitted_multi_model = multi_model.fit()
fitted_multi_model.summary()
여기까지는 전 게시글의 코드와 결과를 복습한 것이다. 이제 다른 변수들 또한 분석하며, 다중공선성 문제를 확인하는 여러 과정을 진행하겠다.
먼저 다중공선성은 절대적으로 어떤 방법으로 확인하는 것이 맞는지, 그리고 어떻게 하면 해결되는지 획일화된 방법이 없다. 그렇기에 아래 3가지 정도의 방법을 통해 다중공선성 확인 과정을 진행하고자 한다.
(1) 결정계수(R^2)와 유의확률(p-value)을 활용한 다중공선성 확인
(2) 상관계수 및 산점도를 통한 다중공선성 확인
(3) VIF를 통한 다중공선성 확인
# crim, rm, lstat, b ,tax ,age, zn, nox, indus 변수를 통한 다중선형회귀분석
## boston data에서 원하는 변수만 뽑아오기
x_data2 = boston[['CRIM','RM', 'LSTAT', 'B', 'TAX', 'AGE', 'ZN', 'NOX', 'INDUS']]
x_data2.head()
# 상수항 추가
x_data2_ = sm.add_constant(x_data2, has_constant = "add")
# 회귀모델 적합
multi_model2 = sm.OLS(target, x_data2_)
fitted_multi_model2 = multi_model2.fit()
# 결과 출력
fitted_multi_model2.summary()
(1) 결정계수(R^2)와 유의확률(p-value)을 활용한 다중공선성 확인
위의 많은 변수를 넣어서 검정한 OLS결과를 보면, "CRIM", "LSTAT", "RM" 세 개만 다중회귀분석을 진행했을 때 OLS결과와 다르다. 가장 큰 부분은 Warnigs에 [2]가 추가된 것이다. 이를 확인하면 강한 다중공선성 또는 다른 numerical 문제가 발생했다고 암시한다.
OLS 검정을 통해보면 기존 3개 변수의 OLS와 비교할 때 R^2(결정계수)는 별로 증가하지 않았다. 게다가 3개 변수의 OLS에서 p-value를 확인하면 0.05보다 작기에 귀무가설(b1 = b2 = b3 = 0)이 기각된다. 하지만, 많은 변수를 넣었을 때, CRIM, AGE, NOX, INDUS 모두 0.05에서 영향이 없다고 판단된다. 하지만, 이 판단은 3개의 OLS검정의 결과와 다르다. 그렇기에 단순 다중공선성이 아니더라도, 변수를 선택할 필요가 있다고 생각된다.
# 세 변수 다중회귀모델의 계수
fitted_multi_model.params

# full모델의 회귀계수
fitted_multi_model2.params
# 3개 모델과 full모델의 잔차비교
import matplotlib.pyplot as plt
fitted_multi_model.resid.plot(label = "3 model")
fitted_multi_model2.resid.plot(label = "full model")
plt.legend()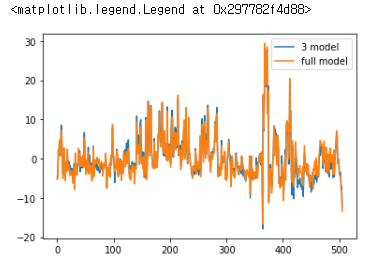
(2) 상관계수 및 산점도를 통한 다중공선성 확인
# 상관행렬 보기
x_data2.corr()

# 상관행렬 시각화
import seaborn as sns #heatmap 만들기 위한 라이브러리
cmap = sns.light_palette("darkgray", as_cmap = True)
sns.heatmap(x_data2.corr(), annot = True, cmap = cmap)
plt.show()
위의 상관행렬과 heatmap을 보면 변수간의 상관관계가 높은 경우가 많은 것을 확인 할 수 있다. 상관관계는 -1~1의 분포를 지니는데 여기서 0.5가 넘어가는 변수들간의 상관관계가 빈출되는 것은 충분히 다중공선성 발생을 의심할 수 있다.
※ seaborn은 시각화 라이브러리로 matplotlib처럼 여러 그래프들을 만들 수 있다. 보통은 상관관계를 위한 pairplot이나 heatmap을 위해서 사용하고, 나머지 boxplot, scatter, line plot 등은 matplotlib을 사용한다. 물론 개인의 편의에 따라 선택적 사용이 가능하다.
# 변수끼리 산점도를 시각화
sns.pairplot(x_data2)
plt.show()

pairplot은 변수간의 산점도를 나타낸 그래프이다. 위의 산점도를 보면 (0,0)~(9,9)로 대칭형태를 띈다. 즉, (0,1)과 (1,0)은 같은 그래프이다. 빨간 박스를 통해 음 또는 양의 상관관계가 시각적으로 보이는 몇개의 산점도를 표시했다. 이를 볼때 이 변수는 관계가 있다고 판단되어 다중공선성을 일으킬 가능성이 높다.
(3) VIF를 통한 다중공선성 확인
VIF는 variance inflation factor의 줄임말로, 다중공선성을 확인할 때 쓰는 지표 중 하나다. variance inflation factor는 말그대로 "분산팽창요인"이다. 보통은 VIF가 10보다 크면 다중공선성이 있다고 판단한다. 하지만, 다른 과정을 함께 거쳐주는 것이 다중공선성 문제 확인의 신뢰성을 높인다.
from statsmodels.stats.ouliers_influence import variance_inflation_factor
# VIF사용을 위한 라이브러리, statsmodels안에 존재한다.
# 사실 모든 통계기법이 statsmodels 모듈에 존재하여
# 이 중에 필요한 통계기법을 찾아 import를 진행하면 된다.
vif = pd.DataFrame()
vif["VIF Factor"] = [varinace_inflation_factor(x_data2.values, i) for i in range(x_data2.shape[1])]
vif["features"] = x_data4.columns
vif

※ RM, B, TAX, AGE, NOX, INDUS 변수들의 VIF가 10보다 크다. vif가 높은 변수가 하나씩 줄어들면 다른 변수들의 vif에도 영향을 미친다. 그래서 변수들을 한 번에 다 제거하기보다는 하나씩 제거하면서 확인해 나아가는 것이 바람직하다.
# nox 변수 제거 후 vif 확인
vif = pd.DataFrame()
x_data3 = x_data2.drop("NOX",axis=1)
vif["VIF Factor"] = [variance_inflation_factor(x_data3.values, i) for i in range(x_data3.shape[1])]
vif["features"] = x_data3.columns
vif
전반적으로 약간씩 VIF가 줄어들었다. 하지만 RM은 여전히 매우 높기에 확실하게 제거할 필요가 있다.
# RM 변수 제거후 VIF확인
vif = pd.DataFrame()
x_data4 = x_data3.drop("RM",axis = 1)
vif["VIF Factor"] = [variance_inflation_factor(x_data4.values, i) for i in range(x_data4.shape[1])]
vif["features"] = x_data4.columns
vif
이제 변수를 제거한 회귀모델을 적합하고 OLS를 확인해보자.
# nox 변수를 제거한 x_data3 상수항 추가 후 회귀모델 적합시키기
# nox, rm 변수를 제거한 x_data4 상수항 추가 후 회귀모델 적합시키기
x_data3_ = sm.add_constant(x_data3, has_constant = "add")
x_data4_ = sm.add_constant(x_data4, has_constant = "add")
model_vif = sm.OLS(target, x_data3_)
fitted_model_vif = model_vif.fit()
model_vif2 = sm.OLS(target,x_data4_)
fitted_model_vif = model_vif2.fit()
# 두 vif를 통한 변수제거 회귀모델의 결과를 비교
fitted_model_vif.summary()

맨 처음 모든 변수를 다 더했을 때 OLS는 condition number가 1.04e+04 였는데 nox변수를 지우고 나서 8.44e+03으로 떨어진 것을 확인 할 수 있다. 다중공선성이 조금은 완화된 것을 확인할 수 있다.
fitted_model_vif2.summary()
위는 NOX와 RM 모두 제거 후 OLS검정 결과인데, 여기서 condition number는 3.85e+03으로 훨씬 더 낮아졌다.
물론 그렇다고 다중공선성이 완전하게 사라진 것은 아니다. 그래도 앞의 모델보다는 더 나은 결과를 보여준다.
시각화와 MSE를 통해 모델의 성능 확인하기
1. 시각화
학습 / 검증데이터 분할
# 학습 검증데이터 분할
from sklearn.model_selection import train_test_split
X = x_data2_
y = target
train_x, test_x, train_y, test_y = train_test_split(X,y, train_size = 0.7, test_size = 0.3, random_state = 1)
# 학습데이터와 검증데이터를 7:3으로 분리한다.
# random_state고정을 통해 그때마다 똑같은 값을 분류하도록 한다.
print(train_x.shape, test_x.shape, train_y.shape, test_y.shape)
# train_x에 상수항 추가 후 최귀모델 적합
fit_train1 = sm.OLS(train_y,train_x)
fit_train1 = fit_train1.fit()
# 검증데이터에 대한 예측값과 true값 비교
plt.plot(np.array(fit_train1.predict(test_x)),label = "pred")
plt.plot(np.array(test_y),label = "true")
plt.legend()
plt.show()
# x_data3와 x_data4 학습 검증데이터 분할
X = x_data3_
y = target
train_x2,test_x2,train_y2,test_y2 = train_test_split(X,y,train_size=0.7, test_size=0.3, random_state=1)
X = x_data4_
y = target
train_x3,test_x3,train_y3,test_y3 = train_test_split(X,y,train_size=0.7, test_size=0.3, random_state=1)
# x_data3/x_data4의 회귀모델 적합 (fit_train2,fit_train3)
fit_train2 = sm.OLS(train_y2,train_x2)
fit_train2 = fit_train2.fit()
fit_train3 = sm.OLS(train_y3,train_x3)
fit_train3 = fit_train3.fit()
# vif를 통해 NOX를 지운 데이터 x_data3 , NOX,RM을 지운 데이터 x_data4 full모델 실제값 비교
plt.plot(np.array(fit_train1.predict(test_x)),label = "pred_full")
plt.plot(np.array(fit_train2.predict(test_x2)),label = "pred_vif")
plt.plot(np.array(fit_train3.predict(test_x3)),label = "pred_vif2")
plt.plot(np.array(test_y2), label = "true")
plt.legend()
plt.show()

2. MSE
from sklearn.metrics import mean_squared_error
#변수 제거가 이루어지지 않은 full모델
mse1 = mean_squared_error(y_true = test_y["Target"], y_pred = fit_train1.predict(test_x))
#변수 NOX만 제거한 모델
mse2 = mean_squared_error(y_true = test_y["Target"], y_pred = fit_train2.predict(test_x2))
#변수 NOX와 RM 두 개를 제거한 모델
mse3 = mean_squared_error(y_true = test_y["Target"], y_pred = fit_train3.predict(test_x3))
print(mse1)
print(mse2)
print(mse3)

MSE print한 결과 변수 NOX만 제거했을 때 MSE가 가장낮고 예측성능이 가장 좋았다. 하지만, 이는 VIF로 확인한 결과와 다르다. "RM"은 "주택당 방의 수"로 Boston 집값의 영향을 충분히 끼칠 것으로 예상된다. 흔히 다중공선성이 발생하는 것은 모델의 예측성능을 떨어뜨린다고 판단하지만, 다중공선성을 명확하게 파악하고 제거하여 이상적인 분석결과를 도출하는 것은 case by case로 다르고, 어려운 일이다.
이처럼 데이터 분석을 할 때, 단순 통계지표를 맹신하는 것이 아니라 개인의 데이터에 대한 이해와 분석에 대한 가설, 그리고 변수를 보는 안목도 매우 중요하다.
'ML in Python > Python' 카테고리의 다른 글
| [Python]로지스틱회귀분석 실습 (2) | 2020.06.20 |
|---|---|
| [Python]변수선택법 실습(2) - 전진선택법/후진소거법/단계적선택법/MAPE 모델 성능 평가 (변수선택법 실습(1)에 전처리과정 존재) (21) | 2020.06.19 |
| [Python]변수선택법 실습(1) - 변수선택법 실습 이전단계, 불필요한 변수 제거 및 가변수 추가 ~ 다중공선성 확인작업 (변수선택법의 코드는 (2)에서) (9) | 2020.06.16 |
| [Python]다중회귀분석 실습 - 데이터 불러오기부터 회귀계수까지 (1) | 2020.06.13 |
| [Python]단순선형회귀분석 실습 - 데이터 불러오기부터 회귀계수까지 (1) | 2020.06.10 |