2020. 7. 16. 18:57ㆍML in Python/Knowledge
이번 게시글은 SVM에 대한 원리와 이해에 집중한다. Python을 통해 구현하는 과정은 아래 링크를 통해서 학습하길 바란다.
https://todayisbetterthanyesterday.tistory.com/32
[Python] SVM(Support Vector Machine)구현 실습
*아래 학습은 Fastcampus의 "머신러닝 A-Z까지"라는 인터넷 강의에서 실습한 내용을 복습하며 학습과정을 공유하고자 복기한 내용입니다. SVM은 다른 분류모형처럼 Decision Boundary를 형성하는 것에 ��
todayisbetterthanyesterday.tistory.com
1. SVM의 직관적 이해
1) SVM의 직관적 이해
SVM은 다른 분류모형처럼 Decision Boundary를 체계적인 방법으로 형성하는 것에 집중한다.

그리고 boundary의 결정은 위의 그림과 같이, 각 분포로부터 margin을 최대화하는 것을 목표로 결정하게 된다. 즉 boundary의 선에 margin을 덧붙여서 최대한 점에 닿지 않도록 margin을 키우는 것이다. 하지만 이러면 분산대비 평균의 차이를 극대화시키는 LDA와는 크게 다른 점이 없어 보인다.
그렇다면 정확하게 구분이 되지 않는 아래와 같은 경우는 어떻게 되는가?

위의 그림을 보면 margin사이에 다른 데이터가 분포하고, 게다가 boundary를 넘어서 다른 집단의 데이터가 분포한다. 이러한 경우는 일반적인 데이터에 매우 많이 존재한다. 오히려 깔끔하게 boudary에 따라 분리되는 데이터를 찾는 경우가 더 힘들수도 있다.
SVM은 이러한 데이터의 경우를 생각하여, 적당한 error를 허용하며, 이러한 error를 최소화하는 boundary를 결정하는 것이다. 그리고 error를 정할 경우 모든 점들을 고려하는 것이 아니라, 선택된 점들만을 선정하여 영향을 끼칠 점과 끼치지 않을 점을 구분한다.
그리고 범주형 변수일 경우 Support Vector Classifier(SVC), 연속형 변수일 경우 Support Vector Regression(SVR)로 SVM의 사용법이 달라진다. 그리고 보통 SVM 자체는 범주형변수일때를 어림잡아서 이야기한다.
2) SVC vs SVR의 직관적인 차이
범주형 변수 : SVC(Support Vector Classification)
가장 큰 차이는 model의 cost에 존재한다.
SVC의 경우 Margin안에 포함된 점들의 error를 기준으로 model cost를 계산한다. 거기에 반대방향으로 분류된, 즉 바운더리를 넘어서 존재하는 점들의 error만을 추가한다. 그림을 보면 아래 노란 부분에 포함된 점들과 boundary의 중심에 위치한 직선과의 error를 계산하는 것이다.

연속형 변수 : SVR(Support Vector Regression)
이와 달리 SVR은 일정 Margin의 범위를 넘어선 점들에 대한 error를 기준으로 model cost를 계산한다. 아래 그림으로 본다면 margin 바깥에 위치한 점들과 차이를 계산하는 빨간선이 곧 한 점에 있어서 error로 계산되는 것이다.

결론적으로 SVM자체는 각 model cost (error)를 최소화하는 boundary를 찾아내는 작업인 것이다.
2. SVM의 수학적 개념

먼저 위와 같은 error가 존재하지 않는/error를 허용하지 않는 상황을 살펴보자
1) SVM에서는 아래와 같은 수식의 초평면을 정의한다.

이때, b와 b0를 유일하게 만들기 위해서 |b| = 1이라는 조건이 필요하다. (b가 다르면 경우마다 다른 해가 나오기 때문)
2) 이 초평면을 정의했을 때, Dicision Rule을 정의한다.
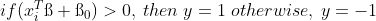
이 Decision Rule은 아래의 경우가 항상 양수가 되도록 만들기 위해 위의 Rule을 정의한 것이다.

다시 말해서, 초평면 > 0 이면, y = 1이어야 위의 수식이 양수가 되고 초평면 < 0일 경우 y = -1이어야 음수가 되기 때문에 위와 같은 Decision Rule이 나왔다.


3) 이렇게 초평면을 정의하는 규칙과 초평면이 정해졌다. 이때 SVM에서 원하는 margin을 최대로 만드는 계수를 구하는 것을 수식으로 표현하면

위와 같이 된다. 즉 y * 초평면이 M보다 클때, b와 b0. |b|=1인 상황에서, M을 최대화하는 것이다. 그리고 이는 다시
3-1) |b|를 최소화 하는 문제로 치환이 될 수 있다. 수식은 아래와 같다.

그리고 이때 |b|를 최소화하는 것은 곧 M을 최대화 하는 것이다.
이제 error를 허용하는 상황을 살펴보자.

1) 초평면은 동일하다
2) 하지만 error가 발생하기에 margin을 고려할 때, 달라진다. margin을 최대화하는 수식은 아래와 같다.


이때 크싸이는 0보다 크며 크사이는 1을 넘길수도 있다.
크싸이가 1을 넘기는 상황은 반대 방향, 즉 바운더리를 넘어 다른집단의 바운더리에 속하는 상황이다.
그리고, 크싸이의 합은 일정 상수보다 작다. 이 일정상수 (constant)는 에러를 허용하는 범위를 지정해주는 것이다. 즉, constant를 너무 크게만들면 너무 큰 error가 발생하게 되는 것이다.
2-1) 이를 다시 달리 표현하면,


다시 |b|를 최소화 하는 문제로 변환된다. 이때도 마찬가지로 M을 최대화 하는 것이다.
이제 이를 Cost Function의 관점으로 바라보자. 에러의 허용치인 크사이의 합은 줄이면서, 허용 에러들을 최소화하는 경우는 trade-off의 관계이다.
1) 이 경우를 수식으로 살펴보면 아래와 같은 제약하의 방정식이 만들어진다. 이 경우를 라그랑지안으로 풀면 해를 도출해낼 수 있다.

2) 이를 라그랑지안 식으로 만들어 미분해서 풀게된다면, 해는 아래와 같다.



3) 위의 해를 구한 것을 라그랑지안으로 치환시켜 새롭게 최적화 식을 정리한다면 아래와 같아진다.

2),3)에서 나온 alpha_i는 알고리즘을 통해 최소화시키는 값을 구할 수 있고 이를 대입하여 초평면을 구할 수 있다.
4) 그 결과, beta_hat은

로 구해진다.
5) 그리고 이때 쿤-터커 조건을 만족한다는 가정을 해준다.
이를 쉽게 말하면, 라그랑지 함수 L의 극소값은 최소값과 일치한다는 가정이다.
6) 그리고 쿤 터커 조건하에 SVM은 아래와 같은 조건을 만족한다.

(1 - 크사이i)를 우측항으로 이동해보면, 즉 에러를 보정했을 때, margin의 위나 바깥에 위치한다는 것이다.
7) 그리고 쿤터커 조건하에

alpha i 와 [괄호 안 식]은 서로 0일때 연산의 결과값으로 0을 갖는다. 이때 alpha i 는 margin끝에 정확히 위치할 때만, 0이 아닌 값을 가질 수 있고, 이때의 점들을 support vector라고 한다.
8) 결론적으로, 마진 끝에 정확히 위치한 점(support vector)들이 정확히

앞에 계산한 beta hat에 합연산이 이루어졌을 때, support vector들로 초평면을 구해내는 것이다.
3. kernel SVM
1) 기존 SVM의 결과는 선형으로 아래와 같이 표시된다.

2) 하지만, kernel SVM은 x의 선형관계를 사용하지 않고 커널을 사용한다는 것이다.

3) 여기서 kernel은
d- degree일 경우 아래와 같다.

< ~ >은 내적을 의미한다.
그리고, Gaussian Kernel(=Radial basis function Kernel)일 경우는 아래와 같다.

커널을 아무렇게 사용하게 된다면, 추정해야되는 모수의 계수가 높아지며 Test error가 높아지고 Overfitting이 발생하는 상황이 생길 수 있다.
그렇기에 단순하게 높은 차원과 더 복잡한 커널을 사용하는 것은 바람직하지 않다.
4. SVM의 장점과 단점
장점
- 데이터의 분포를 모르는 경우 LDA처럼 covariance의 구조를 고려하는 것은 힘들다. 반면 SVM boundary근처의 관측치만 고려하여 LDA보다 데이터의 이해도가 떨어져도 사용할 수 있다.
- 그리고 예측의 정확도가 통상적으로 높다.
단점
- C(에러들에게 부여하는 가중치, 커지면 에러를 최대한 범하지 말아야하고 작아지면 에러를 많이 허용한다는 것) 를 결정해야한다. 이는 경험적인 과정이기에 정답이 없다.
- parameter의 결정과 모형의 구축에 시간이 오래걸린다.
'ML in Python > Knowledge' 카테고리의 다른 글
| [Data Analysis 개념] Decision Tree(의사결정나무) 모형 - Classification/Regression Tree의 직관적/수학적 이해 (0) | 2020.07.19 |
|---|---|
| [Data Analysis 개념] 시계열 분석 - AR/MA/ARIMA/분해시계열 의미 (0) | 2020.07.18 |
| [Data Analysis 개념] LDA와 QDA의 이해 (1) | 2020.07.09 |
| [Data Analysis 개념] 차원 축소법 - PCA(주성분 분석) (0) | 2020.07.07 |
| [Data Analysis 개념] k-Fold Cross Validation (0) | 2020.07.03 |