[Python] DBSCAN clustering

 

 이 게시글은 오로지 파이썬을 통한 실습만을 진행한다. DBSCAN 군집분석의 개념 및 원리를 알고자하면 아래 링크를 통해학습을 진행하면 된다. 

https://todayisbetterthanyesterday.tistory.com/59

[Data Analysis 개념] Clustering(2) - Hierarchical clustering / DBSCAN

 

실습 데이터 Load & Dataframe 변환

from sklearn import datasets
import pandas as pd

iris = datasets.load_iris()
labels = pd.DataFrame(iris.target)
labels.columns=['labels']
data = pd.DataFrame(iris.data)
data.columns=['Sepal length','Sepal width','Petal length','Petal width']
data = pd.concat([data,labels],axis=1)

data.head()

 

Feature Data

feature = data[ ['Sepal length','Sepal width','Petal length','Petal width']]
feature.head()

 여기까지 실습데이터를 DBSCAN 모델에 적용시킬 준비를 하였다. 우리는 4가지 변수를 갖고 분석을 진행할 것이다. 

DBSCAN fitting

from sklearn.cluster import DBSCAN
import matplotlib.pyplot  as plt
import seaborn as sns

# create model and prediction
model = DBSCAN(eps=0.5,min_samples=5)
predict = pd.DataFrame(model.fit_predict(feature))
predict.columns=['predict']

# concatenate labels to df as a new column
r = pd.concat([feature,predict],axis=1)

print(r)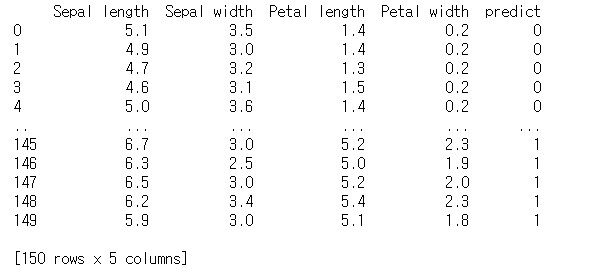

 위에서 DBSCAN model을 정의할 때, parameter로 eps=0.5, min_sample=5를 지정해 주었다. DBSCAN은 K-means와 달리 처음에 군집의 개수를 정의하지 않는다. 자동적으로 최적의 군집개수를 찾아나가는 알고리즘이다. eps는 여기서 한 데이터가 주변에 얼만큼 떨어진 거리를 같은 군집으로 생각할지의 기준에서 거리이다. 그리고 min_samples는 적어도 한 군집에는 5개의 sample들이 모여야 군집으로 인정한다는 것이다. 

 이를 이미지로 표현하면 아래와 같다. 

 여기서 eps는 반지름의 크기를 말하는 것이다. 이를 토대로 군집형성을 진행하였으며, clustering의 경우는 비지도학습이기 때문에 predict를 raw data와 대조하지 않는다. 실제로 군집분석을 진행할 때는 predict를 할 target데이터가 존재하지 않기 때문이다. 

 예측된 군집은 아래의 형태와 같다. 

 

Pair plot

#pairplot with Seaborn
sns.pairplot(r,hue='predict')
plt.show()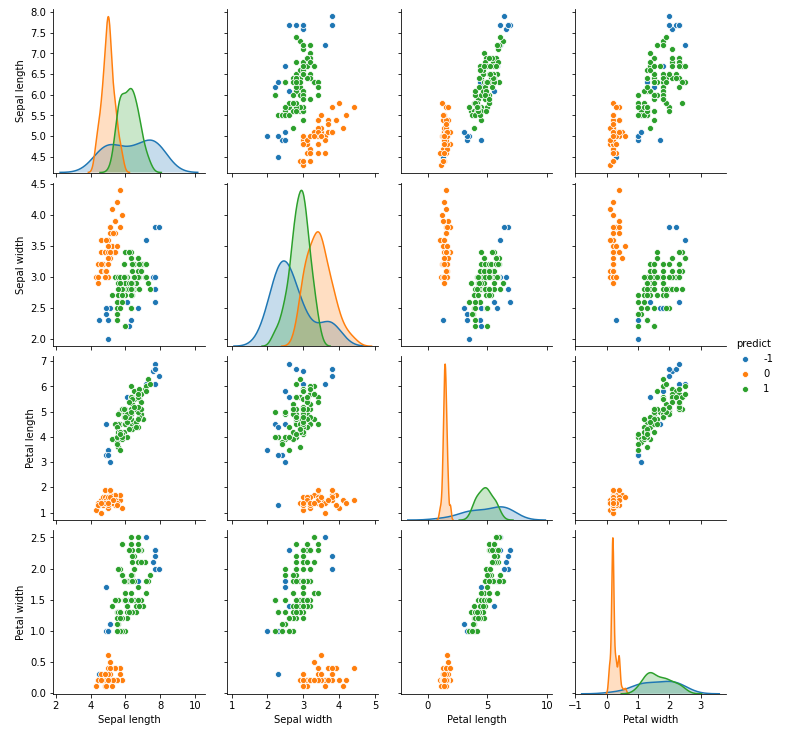

 위의 결과는 예측된 군집을 sns라이브러리의 pairplot으로 표현한 것이다. 그리고 아래 데이터는 실제 군집이다. 차이가 좀 심하게 나는듯하다. 이 데이터의 특성에 DBSCAN이 잘 맞는다고 말할 수 없다. 실제로 K-means는 원형데이터들에게 잘 맞는다. 그리고 위/아래와 같이 너무 가까운 거리에 군집 여러개가 함께 있을 때 DBSCAN은 잘 구분을 해내지 못한다. 

 DBSCAN은 한 점에서 계속적으로 이동해나가며 주변의 기준만큼 가까운 점들을 찾아서 번져가기 때문에 너무 sample들간의 거리가 가까우면 같은 군집으로 취급을 해버린다.  

#pairplot with Seaborn
sns.pairplot(data,hue='labels')
plt.show()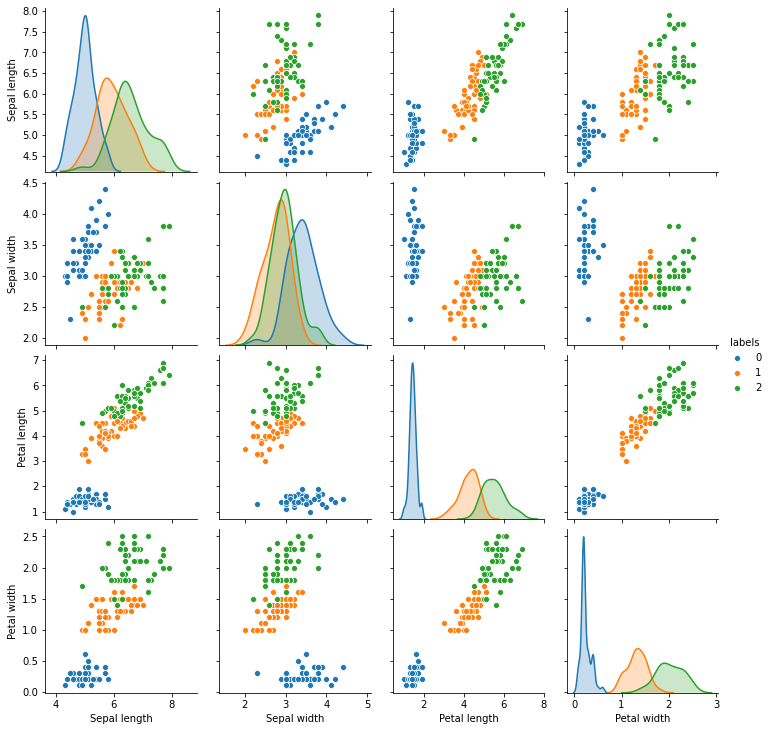

  

 아래 과정은 K-means를 통해서 군집분석(clustering)을 진행하는 것이다. 아래는 기존 데이터가 3개의 군집이 있다는 것을 알기에 3개의 클러스터를 parameter로 지정해주고(n_clusters=3) fitting을 하였다. 

from sklearn.cluster import KMeans
km = KMeans(n_clusters = 3, n_jobs = 4, random_state=21)
km.fit(feature)

new_labels =pd.DataFrame(km.labels_)
new_labels.columns=['predict']

r2 = pd.concat([feature,new_labels],axis=1)

#pairplot with Seaborn
sns.pairplot(r2,hue='predict')
plt.show()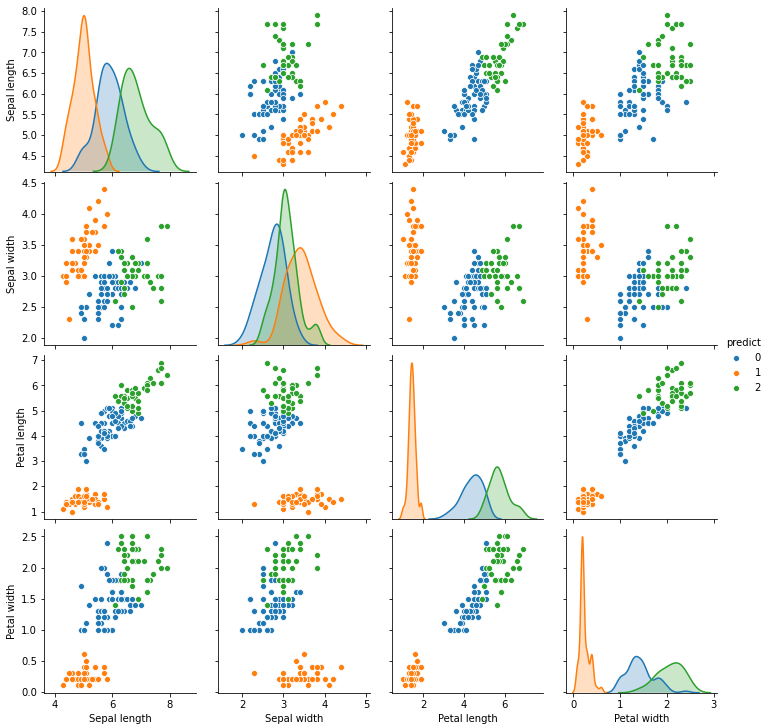

 결과를 보면 K-means가 DBSCAN보다 훨씬 성능이 좋은 듯 하다. 하지만 이는 이 데이터의 특수성 때문인 것이다. 머신러닝 모델도 그렇듯이 군집분석 또한 항상 가장 나은 모델은 없다. 데이터에 맞는 특정 모델을 맞추어 사용할 필요가 있다.

 이제 다른 실습 데이터를 통해서 K-means와 DBSCAN을 비교해보자. 실습데이터는 numpy파일이다. python은 매우 편리한게 pickle 및 다른 라이브러리들을 활용하여 변수 그 자체를 저장할 수 있다. 실습을 진행하고자 한다면 아래 데이터를 같은 경로에 다운받으면 된다.

clusterable_data.npy

0.04MB

 

New data practice

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn.cluster as cluster
import time
%matplotlib inline
sns.set_context('poster')
sns.set_color_codes()
plot_kwds = {'alpha' : 0.25, 's' : 80, 'linewidths':0}

data = np.load('./clusterable_data.npy')

plt.scatter(data.T[0], data.T[1], c='b', **plot_kwds)
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)

 실습데이터를 scatter plot으로 표현하였다. 눈으로 보기에 크게 5가지의 군집이 존재하는것처럼 보인다. 그 외의 잡음(noise)가 꽤나 많이 분포한다. 이 데이터를 시각화를 통해 비교해보자. 

def plot_clusters(data, algorithm, args, kwds):
    start_time = time.time()
    labels = algorithm(*args, **kwds).fit_predict(data)
    end_time = time.time()
    palette = sns.color_palette('deep', np.unique(labels).max() + 1)
    colors = [palette[x] if x >= 0 else (0.0, 0.0, 0.0) for x in labels]
    plt.scatter(data.T[0], data.T[1], c=colors, **plot_kwds)
    frame = plt.gca()
    frame.axes.get_xaxis().set_visible(False)
    frame.axes.get_yaxis().set_visible(False)
    plt.title('Clusters found by {}'.format(str(algorithm.__name__)), fontsize=24)
    plt.text(-0.5, 0.7, 'Clustering took {:.2f} s'.format(end_time - start_time), fontsize=14)

 위의 user defined function은 cluster 결과를 scatter plot으로 구현하는 함수이다. 이 함수를 통해서 아래 결과들을 살펴보자. 

 

K-means

plot_clusters(data, cluster.KMeans, (), {'n_clusters':3})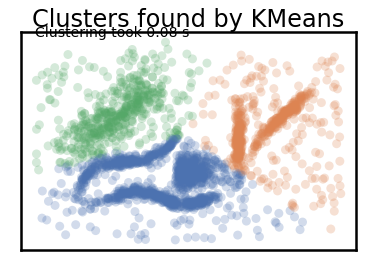

 K-means를 통해 만든 K=3 clustering이다. 

plot_clusters(data, cluster.KMeans, (), {'n_clusters':4})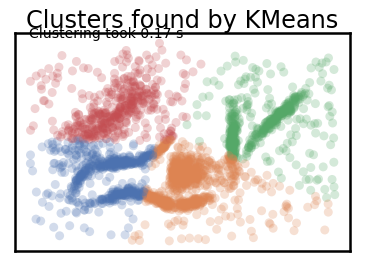

 K-means를 통해 만든 K=4 clustering이다. 

plot_clusters(data, cluster.KMeans, (), {'n_clusters':5})

K-means를 통해 만든 K=5 clustering이다. 

plot_clusters(data, cluster.KMeans, (), {'n_clusters':6})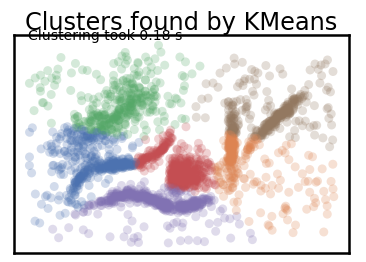

K-means를 통해 만든 K=6 clustering이다. 

 

DBSCAN

plot_clusters(data, cluster.DBSCAN, (), {'eps':0.020})

 위의 결과는 eps(epsilon) 즉 거리를 0.02 기준으로 분포한 데이터를 군집화시킨 DBSCAN이다. 결과적으로 크게 5가지의 cluster가 형성된 것으로 보인다. 

plot_clusters(data, cluster.DBSCAN, (), {'eps':0.03})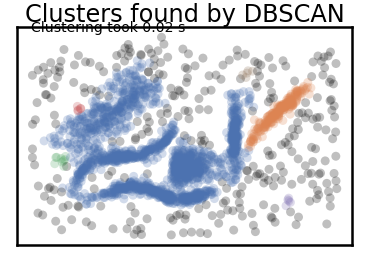

 위의 결과는 eps(epsilon) 즉 거리를 0.03 기준으로 분포한 데이터를 군집화시킨 DBSCAN이다. 결과적으로 크게 2가지의 cluster가 형성된 것으로 보인다. 

 위의 차이를 확인해보자. 먼저 K-means에는 이상치로 판단된 sample이 존재하지 않았다. 즉, 회색부분이 존재하지 않았다. 이 원인은 K-means는 중심점을 잡고 전반적인 데이터들의 거리를 평균 계산하여 군집을 형성하기 때문이다. 

 반면 DBSCAN은 회색부분이 많다. 주된 영역을 제외하면 모두 회색이다. 이는 한 sample에서 다른 sample간 1대1 거리계산을 통해서 군집을 확장시켜나가기때문에 일정 거리(epsilon)이 넘어가면 이상치로 판단하기 때문이다. 그렇기에 확실하게 K-means보다는 이상치에 덜 민감하다. 하지만, eps parameter를 잘 선택해야한다는 문제가 있다. eps를 잘 선택하는 것 또한 K-means에서 최적의 K를 찾는 것 만큼 힘들다.  

 

dbs = DBSCAN(eps=0.03)
dbs2=dbs.fit(data)
dbs2.labels_

 DBSCAN으로 형성한 군집분석의 결과는 다른 clustering 모델과 동일하게 labels 함수를 통해서 알아낼 수 있다. 

 

 마지막으로 DBSCAN의 upgrade version인 HDBSCAN모델이 있다. HDBSCAN은 DBSCAN보다 하이퍼 파라미터(eps, min_samples)에 덜 민감하다는 장점이 있다. 

import hdbscan

clusterer = hdbscan.HDBSCAN(min_cluster_size=15, gen_min_span_tree=True)
clusterer.fit(data)

palette = sns.color_palette()
cluster_colors = [sns.desaturate(palette[col], sat)
                  if col >= 0 else (0.3,0.3,0.3) for col, sat in
                  zip(clusterer.labels_, clusterer.probabilities_)]
plt.scatter(data.T[0], data.T[1], c=cluster_colors, **plot_kwds)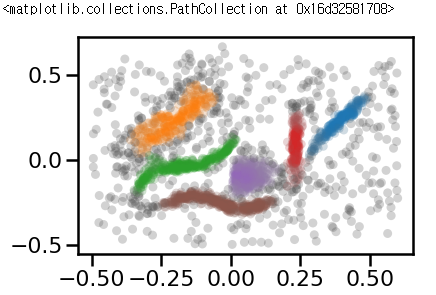

 HDBSCAN의 결과를 보면 이상치를 건드리지 않는다. 물론 만약 저 분포된 회색점들이 이상치가 아니라면 DBSCAN종류는 알맞는 모델이 아니다. 여튼 크게 6가지의 cluster가 잘 형성된 것을 볼 수 있고 거리가 가깝더라도 cluster구분이 확실하게 DBSCAN보다 나은 결과를 보인다.