[Data Analysis 개념] Clustering(2) - Hierarchical clustering / DBSCAN
https://todayisbetterthanyesterday.tistory.com/58
[Data Analysis 개념] Clustering(1) - K-means/K-medoids
1. Clustering - 군집분석 군집분석은 비지도학습(unsupervised learning)의 일종으로 유사한 데이터끼리 그룹화를 시키는 학습모델을 말한다. 각 데이터의 유사성을 측정하여, 유사성이 높은 집단끼리 �
todayisbetterthanyesterday.tistory.com
앞의 게시글을 통해서 Clustering의 설명과 K-means/K-medoids clustering에 대해서 알아보았다. 이번 게시글은 Hierarchical clustering과 DBSCAN에 대해서 알아보자.
1. Hierarchical clustering
Hierarchical clustering은 개체들을 가까운 집단부터 순차적이고 계층적으로 차근차근 묶어나가는 방식이다. 이러한 방식으로 군집이 형성되기에 유사한 개체들이 결합되는 dendogram을 통해서 시각화가 가능하고, 계층적 구조로 인해 사전에 군집의 개수를 정하지 않아도 수행이 가능하다.
하지만, 군집을 형성하는데 있어서 Hierarchical clustering은 매 단계에서 지역적 최적해(local minimum)을 찾아가는 방법을 사용하기에 결과가 전역적 최적해(global minimum)이라고 볼 수 없다.

Hierarchical clustering이 학습되는 과정은 아래와 같다.
1. 모든 개체들 사이의 거리에 대한 유사도 행렬 계산
2. 거리가 인접한 관측치끼리 cluster 형성
3. 유사도 행렬 업데이트
아래의 예시를 봐보자.
먼저 처음의 유사도 행렬이 만들어졌다. 이때 A와 가장 거리상 유사한 점은 D이다. 이 두 관측치를 한 cluster로 묶는다.
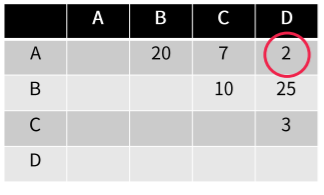
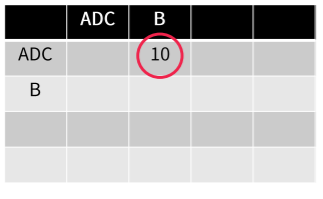
A와 D가 한 cluster로 묶였다. 그러면 유사도 행렬은 AD로 업데이트 된다. 이제 업데이트된 유사도 행렬에서 가장 가까운 관측치는 C이다. 이 C를 다시 clustering한다. 이것을 계속 반복한다.

그리고 남은 관측치들이 모두 클러스터링이 되면 학습을 종료한다.
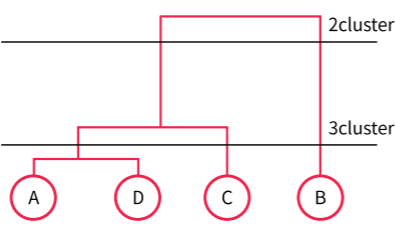
최종적으로 도출된 결과는 아래의 Tree형태와 같다. 이때, 군집을 2개 형성한다면, ADC/B와 같이 나뉠 것이고, 군집을 3개 형성한다면, AD/C/B로 나뉠 것이다. 이것은 거리를 기반한 유사도로 만들어졌다.
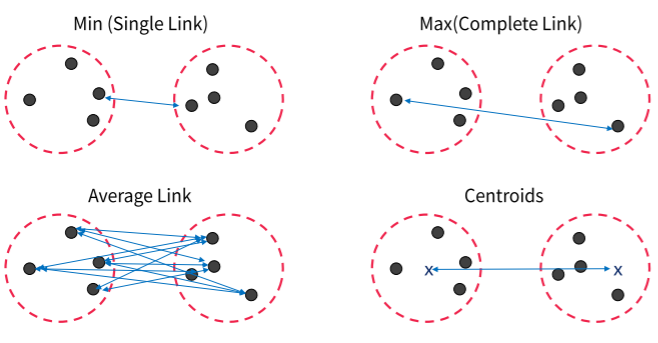
Hierarchical clustering에도 K-means/K-medoids처럼 거리를 선택할 수 있다. 가장 가까운 Min, 가장 멀리 떨어진 Max, 평균, 중앙점 비교를 모두 유사도 행렬상에서 clustering간의 거리로 활용할 수 있다.
그리고 추가적으로 Ward's method가 있다. Ward's method는 두 개의 클러스터가 병합되었을 때 증가되는 변동성의 양을 기준으로 하는 방법이다. 수식으로 표현하면 아래와 같다.
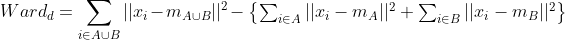
아래의 이미지를 보자. 왼쪽 예시는 두 개의 클러스터가 상대적으로 더 떨어져있는 예시이다. 오른쪽에 비해서 변동성이 큰 것이다. 그렇기에 ward distance는 더 크다. 반면 오른쪽은 더 가깝기에 ward distance는 더 작게 표현된다.
2. DBSCAN clustering
K-means clustering은 초기 중심으로 설정한 값에 크게 영향을 받고 노이즈와 아웃라이어에 민감하다는 단점을 가졌었다. 그리고 군집의 개수 K를 설정하는 것도 쉽지 않다는 단점이 있었다. 이러한 단점을 상대적으로 극복한 것이 DBSCAN clustering이다.
DBSCAN은 Density-based Spatial Clustering of Applications with Noise의 줄임말로 2014년 KDD 학회에서 상을 받은 군집분석 알고리즘이다. 그리고 Density-based clustering 중에서 가장 유명하고 성능이 우수하다고 알려져있다.
DBSCAN의 가장 대표적인 특징은 eps-neighbors와 MinPts를 사용하여 군집을 구성한다는 것이다. Eps-neighbors는 한 데이터를 중심으로 epsilon 거리 이내에 데이터를 한 군집으로 구성한다고 명시하는 parameter이다. MinPts는 한 군집은 MinPts보다 많거나 같은 수의 데이터로 구성된다는 것이다. 만약 MinPts보다 적은 수의 데이터가 eps-neighbors를 형성하면 noise로 취급을 한다. 즉, 군집은 최소한의 일정 데이터수를 유지해야한다는 것이다.
DBSCAN의 학습과정은 아래의 그림을 통해서 알 수 있다.
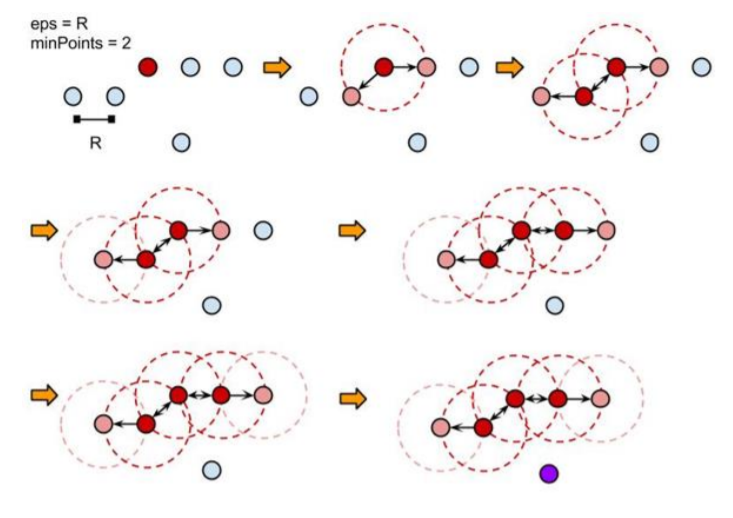
사용자는 eps와 minPoints를 parameter로 지정한다. 군집이 형성될 개수K를 parameter로 설정하지 않는 것이다. 그리고 eps를 반지름하는 원 안에 있는 관측치를 찾는다. 찾으면 그 관측치를 군집내 포함시키고, 해당 관측치를 기준으로 다시 관측치를 찾아나선다. 이 군집이 최소한의 관측치 개수 minPoints를 넘기면 군집으로 인정이 되는 것이다. 그리고 연결되지 않은 관측치들은 이상치로 분류한다.
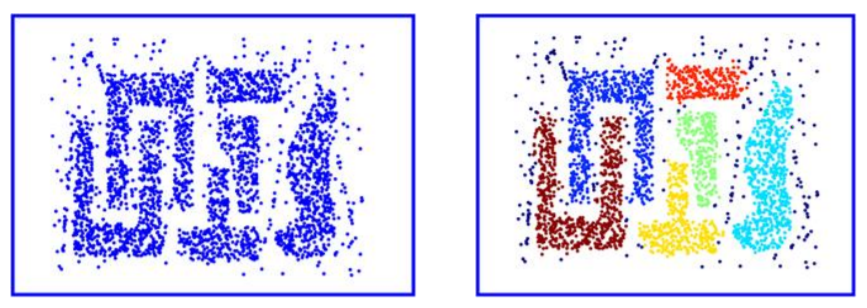
DBSCAN의 가장 큰 장점은 원형이 아닌 데이터들의 군집을 잘 분류해내고, 이상치에 반응을 하지 않는다는 것이다. 그리고 K-means/medoids처럼 군집의 수를 설정할 필요가 없다.
하지만, 하나의 데이터는 한 군집에 속해야 하는데, 이는 시작점에 따라 다른 군집으로 형성될 가능성이 존재한다. 그리고 Eps의 크기에 의해 DBSCAN의 성능이 크게 좌우된다. 게다가 eps를 기준으로 하기에 군집별로 밀도가 다를 경우 DBSCAN은 군집화를 제대로 수행하지 못할 가능성이 크다.
그렇기에 Eps와 MinPoints parameter를 잘 설정할 필요가 있다. 이는 데이터에 대한 이해도가 충분할 경우에 상대적으로 쉬워진다. Minpoints는 가장 기본적으로는 변수의 수 + 1로 이루어진다. 그리고 최소한 3이상으로 설정할 필요가 있다. 왜냐하면, 1인 경우는 데이터 하나하나가 모두 군집인 것으로 판단이 되기 때문이다.
Eps설정의 경우에는 eps가 너무 작을경우 상당 수의 데이터가 노이즈로 구분되어 무시될 수 있다. 그렇다고 너무 클 경우는 모든 데이터가 하나의 군집으로 될 수도 있다. 그렇기에 eps를 잘 설정하는 것이 중요하다. 일반적으로 K-nearest neighbor 그래프의 distances를 그래프로 나타낸 후 거리가 급격하게 증가하는 지점을 eps로 설정하는 방법이 존재한다.
Hierarchical clustering과 DBSCAN에 대한 실습과정은 아래 링크를 통해 남겨놓겠다.
https://todayisbetterthanyesterday.tistory.com/61
[Python] Hierarchical clustering(계층적 군집분석)
*아래 학습은 Fastcampus의 "머신러닝 A-Z까지"라는 인터넷 강의에서 실습한 내용을 복습하며 학습과정을 공유하고자 복기한 내용입니다. 이 게시글은 오로지 파이썬을 통한 실습만을 진행한다. Hi
todayisbetterthanyesterday.tistory.com
https://todayisbetterthanyesterday.tistory.com/62
[Python] DBSCAN clustering
*아래 학습은 Fastcampus의 "머신러닝 A-Z까지"라는 인터넷 강의에서 실습한 내용을 복습하며 학습과정을 공유하고자 복기한 내용입니다. 이 게시글은 오로지 파이썬을 통한 실습만을 진행한다. DB
todayisbetterthanyesterday.tistory.com