[Data Analysis 개념] 차원 축소법 - PCA(주성분 분석)

 이 게시글은 PCA의 이해와 수학적 과정만을 다룬다. Python 실습코드를 따라가보면 훨씬 이해가 잘 될 것이다. 아래 링크를 남겨놓겠다.

https://todayisbetterthanyesterday.tistory.com/16

[Python] - PCA(주성분분석) 실습

 

 

---

 

 데이터 분석을 진행할 때 발생할 가능성이 높은 문제(특히, KNN에서) "차원의 저주". 이를 해결하려면 어떻게 해야하나?

차원의 저주라는 개념을 모른다면 아래 링크를 통해 이전 게시글을 공유하겠다.

https://todayisbetterthanyesterday.tistory.com/15?category=822147

[Data Analysis 개념] 차원의 저주

 

 차원을 줄이는 방법에는 여러가지가 있다. 변수 선택법, Ridge, Rasso, 상관계수가 높은 변수 중 일부를 제외하는 방법 등 여러 가지가 있다. 

 하지만, 상관계수가 높은 변수를 제외하면 정보의 손실이 발생한다. 예를 들어, 상관계수가 0.8이라고 한다면 0.2에 해당하는 정보는 버려지게 되는 것이다.

 그렇기에 차원을 줄이면서 정보의 손실을 최소화 하는 방법이 바로 PCA(주성분분석)이다. PCA의 기본적인 원리는 행렬연산으로 이루어져 있다. 그렇기에 PCA에 대해 알아보기 위해 수학적 수식의 과정이 많이 등장할 것이다.

공분산 행렬

 공분산 행렬이란 쉽게 말해 변수들간의 상관관계를 행렬로 표현한 것이다. 공분산 행렬의 형태는 아래 행렬과 같다. 

공분산 행렬

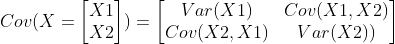
 만약 X1과 X2 사이의 음의 상관관계가 있다고 하자. 그러면 공분산행렬은 아래의 예시와 같은 부호를 띌 것이다.

예시)

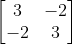
 그리고 X가 centering되어 있다면, 즉 평균이 0으로 맞추어져 있다면, 공분산 행렬은 아래와 같은 수식으로 표현된다.

공분산 행렬 수식

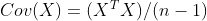
 아래와 같은 행렬의 분포 "A"가 있다고 하자. 공분산 행렬은 아래와 같은 점들과 내적연산을 통해 점의 위치를 이동시키는 결과를 낳는다. 

예시

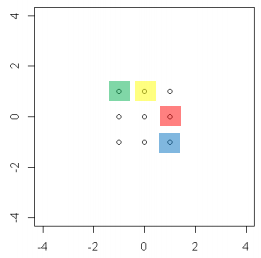
1. "A"에다가, 일반적인 공분산 행렬과 내적연산을 진행한 경우

 위의 이미지는 공분산행렬과 내적연산을 진행한 결과다. 점들의 분포가 넓어졌지만, 색칠된 점들간의 상대적인 위치는 동일한 상태이다.

2. "A"에다가, 대칭행렬이지만 Positive definite이 아닌 행렬과 내적연산을 진행한 경우

 위의 이미지는 Positive definite이 아닌 행렬(일반적으로 말하는 공분산행렬X)과 내적연산을 진행한 결과이다. 순서는 같지만, 위아래의 위치가 변화되었다.

3. "A"에다가, 행렬식이 0인 행렬을 내적연산한 경우

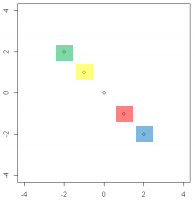
 위의 이미지는 행렬식이 0일 경우, 점들과의 내적연산은 선형관계를 이루는 형태로 만든다.

 

PCA ( Principal Conponents Analysis : 주성분 분석 )

 

 PCA를 알기 위해서는 이러한 공분산행렬의 특성을 알고 갈 필요가 있다. 우리는 기존 데이터(샘플의 분포행렬)에 Singular-Value-Decomposition(SVD)를 통해 eigen vector와 eigen value를 구할 수 있다. 그리고 이를 통해 Centering된 데이터에 eigen vector를 내적연산 시키는 것이 바로 PCA이다.

 쉽게 말해서, 편향되지 않은 상태의 데이터를 위의 공분산행렬의 내적연산처럼 가공하여 새롭게 설명력을 가진 축을 만들어 내는 것이다. 그리고 이 새로운 축에 내린 정사영이 바로 "Principal Components = PC = PCscore" 이다.

빨간선 - 새로운 축을 도출 / 초록선 - 새로운 축에 내린 정사영 (PCscore)

y축(target)을 PCscore로 변경했을 때

 그러한 PCA는 언제 사용하는가? Feature의 변수가 여러개 있는 경우에 변수의 개수를 줄이면서 줄어든 변수로 인한 정보의 손실을 최소화하고 싶을 때, 즉 차원을 줄이면서 정보의 손실을 최소화하고자 PCA를 사용한다.

PCA의 수학적 정의

 Eigen value / Eigen vector

 아래 수식을 만족할 경우

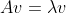
 v는 고유벡터(eigen vector), lambda는 고유값(eigen value)라고 한다.  그리고 아래의 그림과 같이 A는 v를 선형변환한다. 

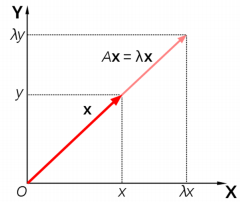
 즉, 임의의 점에 대해서 "A"라는 transformation을 시행할 때, 고유벡터의 방향은 바뀌지 않는다는 것을 의미한다. 그리고 고 고유값은 변해지는 스케일의 정도이다(길이상). 

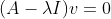
 위의 식을 좌변으로 넘기면 고유벡터 v가 존재하기 위해서는 A-lambda*I가 역행렬이 존재하지 않아야 한다. 이때 이식의 판별식이 "0"이라는 연산을 통해 고유값과 고유벡터를 결정할 수 있다.

 이로써,  고유값과 고유벡터에 대한 개념 또한 알아보았다. 

 Singular-Value-Decomposition (SVD)

1.

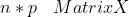
 n x p 행렬 X 가 있다고 하자. 

2.

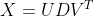
 이 n x p 형태를 U*D*transpose(V)로 나누는 것이 바로 SVD이다.

3.

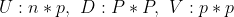
각 U, D, V, 즉 Singular value의 형태는 위와 같다.

4.

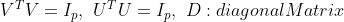
 이때 이 U,D,V는 위의 조건을 만족시킨다. 그리고, 

 1. V의 컬럼벡터는 transpose(X)*X의 eigen vectors이고

 2. D의 대각 원소(Diagonal entries)는 transpose(X)*X의 eigen values이다.

 

 이와 같이 SVD를 통하여, 특정 matrix의 공분산 구조행렬의 eigen vector와 eigen value를 얻어낼 수 있고, X가  centering되어 있을 때, transpose(X)*X는 X의 공분산 구조이다.

 이제 사실상 PCA를 다했다. 이를 이제부터 적용해보면, 

 

 PCA 수행과정

 

1. Feature "X"는 먼저 Mean centering 되어야한다. 

2. SVD 수행을 통해 centering된 "X"를 U*D*transpose(V)로 분리시킨다.

3. SVD 결과를 활용하여, 공분산의 eigen vector와 eigen value를 구할 수 있다.

4. centering된 X에 eigen vector를 내적한 것이 바로 PCscore이다. 

5. 즉, PCscore = XV = UD 이다.

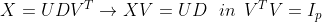
6. 마지막으로, 설명변수 X가 아니라, PCscore를 활용하여 분석을 진행한다. 

 

추가적인 의문사항이 있으면 답글을 통해서 QnA를 진행하겠습니다.